| |
Solve for x: |
Answer |
1. |
|
|
• Take e of both sides to eliminate the ln
• Remember that ex and ln x are inverse function (one undoes the other). |
|
2. |
|
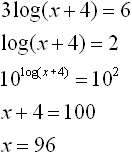 |
• Isolate the log expression
• Choose base 10 to correspond with log (base 10)
• Apply composition of inverses and solve. |
|
3. |
|
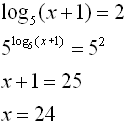 |
• Choose base 5 to correspond with the log base of 5.
|
|
4. |
|
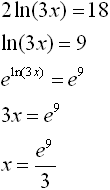 |
• Isolate the ln expression first. |
|
5. |
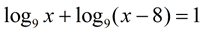 |
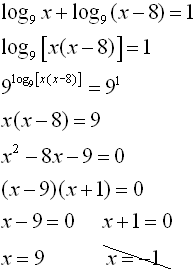 |

• You will need to use the log properties to express the two terms on the left as a single term.
• Remember that log of a negative value is not a real number and is not considered a solution. |
|
6. |
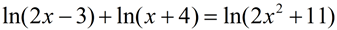 |
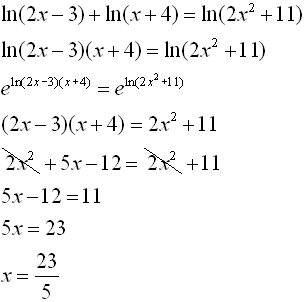 |
7. |
Using your graphing calculator, solve for x to the nearest hundredth.
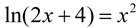 Method 2: Place the left side of the equation into Y1 and the right side into Y2. Under the CALC menu, use #5 Intersect to find where the two graphs intersect.
Method 2: Place the left side of the equation into Y1 and the right side into Y2. Under the CALC menu, use #5 Intersect to find where the two graphs intersect.
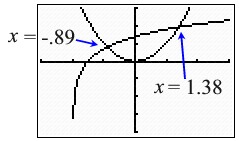
|
Method 1: Rewrite so the equation equals 0.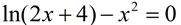
Find the zeros of the function.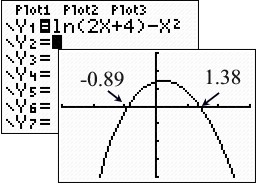
Both values are solutions, since both values allow for the ln of a positive value. |