|
Let's review, and extend, what we saw in Algebra 1 regarding factoring higher powers.
We know that some factoring problems involving higher powers can be rewritten as a simpler factoring problem.
 Not all polynomial expressions are factorable. Not all polynomial expressions are factorable.
Are there Common Factors? |
|
This first example creates a simpler problem by first finding a common factor. |
Factor: 2x5 - 9x4 - 5x3 |
Look carefully! Each of these terms has a factor of x3. Factoring out x3 may create a problem which can be factored further.
x3(2x2 - 9x - 5) |
The remaining trinomial can be easily factored.
Factor: x3(2x2 - 9x - 5) = x3(2x + 1)(x - 5) ANSWER
|
|
This second example deals with multiple variables by also finding the common factor. |
Factor: x4y2 - 4x3y2 - 12x2y2 |
Don't be distracted by the fact that this problem looks difficult. Examine each term to see if there is a common factor, which when factored out may also leave another factorable expression.
The common factor in each term is x2y2.
x2y2 (x2 - 4x - 12)
x2y2 (x - 6)(x + 2) ANSWER
|

Is there a quadratic-style pattern? |
|
This example replaces sections of the problem with a new variable that will create a factorable quadratic. This process may be referred to as factoring using substitution. |
Factor: a4 + a2 - 12 |
At first glance, this problem doesn't look like anything we have seen. But upon closer examination, this is really a very simple problem that we already know how to solve. The trick is to look at the problem in a slightly different manner. If the powers of a are rewritten, we see a quadratic.
a4 + a2 - 12 = (a2)2 + (a2) - 12
If you now replace a2 with x (or your favorite variable letter), the problem becomes very familiar. |
Let a2 = x and substitute. (a2)2 + (a2) - 12 = x2 + x - 12
|
Factor the new form: x2 + x - 12 = (x + 4)(x - 3)
|
Re-substitute x = a2. (x + 4)(x - 3) = (a2 + 4)(a2 - 3) ANSWER |
Did you notice the pattern of looking for a hidden quadratic? In this one variable trinomial, the power in the middle term is half the power in the leading term. The power values need not be "even" numbers. The leading power just needs to be twice as large.

Are there Only Even Powers? |
|
Even powers in an expression may mean that the expression can be written as a "perfect square", and factored using the square root of the expression. |
Factor: x10 - 4 |
x10 and 4 are perfect squares. The expression can be re-written and solved by factoring the difference of the perfect squares.
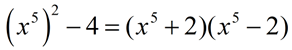 ANSWER ANSWER
|
|
In this example, after using the difference of perfect squares, further factoring will be needed to arrive at the final answer. |
Factor: m8 - 16 |
Since m8 and 16 are perfect squares, and this problem deals with subtraction, we are looking at factoring the difference of perfect squares. (m4 - 4)(m4 + 4)
But the first of the two factors is ANOTHER difference of perfect squares. Repeat process. (m2 - 2)(m2 + 2)(m4 + 4) ANSWER |
|
This example shows the problem from Example 5 being solved by another method: the substitution approach. |
Factor: m8 - 16 |
This problem can also be solved using the substitution approach.
(m4)2 - 16
Let m4 = x. (m4)2 - 16 = (x)2 - 16
Factor: (x)2 - 16 = (x - 4)(x + 4)
Re-substitute: (x - 4)(x + 4) = (m4 - 4)(m4+ 4)
Repeat process:
(m2)2 - 4
Let m2 = b. (m2)2 - 4 = (b)2 - 4
Factor:
(b)2 - 4 = (b- 2)(b+ 2)
Re-substitute: (b- 2)(b+ 2) = (m2- 2)(m2+ 2)
Total answer:
(m2 - 2)(m2 + 2)(m4 + 4) ANSWER
|

Is there a variable in the power? |
|
This is a tough one!! What happens if there is a variable in the exponent? |
Factor: x 2p + 2x p - 24 |
You have to be a bit more creative to see this solution. The secret is in the exponents.
x p • x p = x 2p making x 2p the square of x p. A substitution will solve our problem.
(x p )2 + 2(x p ) - 24
|
Let x p = a and substitute. (x p)2 + 2(x p) - 24 = a2 + 2a - 24
|
Factor the new form: a2 + 2a - 24 = (a - 4)(a + 6)
|
Re-substitute a = x p. (a - 4)(a + 6) = (x p - 4)(x p+ 6) ANSWER
NOTE: Without further information about "p", we do not know if further factoring is needed. If p were a positive even exponent, (x p - 4) could be the difference of two squares and could be factored further. However, without that information, we stop at our labeled answer. |

We will see more examples of factoring higher power polynomials when we deal with solving polynomial equations in the section Polynomial Equations.
Historical note: Mathematicians have been unable to devise an exact general method for factoring a polynomial. Factoring techniques (formulas) are known for "special" polynomials such as linear (degree 1), quadratic (degree 2), cubic (degree 3), and quartic (degree 4). Mathematician Evariste Galois (1811-1832) proved that there will never be a general formula to factor polynomials of degree five or higher.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|