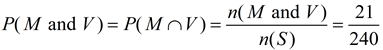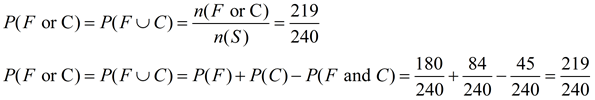|
We saw the following two-way frequency table in Algebra 1. Two hundred and forty people were surveyed as to their preference for a sport utility vehicle (SUV) or a sports car. |
 |
Two Way Frequency Table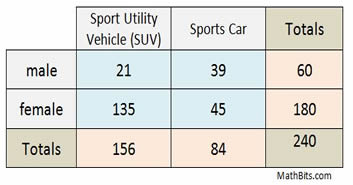 |
Let's take a look at how two way frequency tables are associated with probability.
Let's apply our probability "vocabulary" to the table. There are four possible "events" occurring, that we can also refer to as "sets":
| M = male |
F = female |
| V = Sport Utility Vehicle |
C = Sports Car |
|
 Task 1: Find the "number" of Total values for the four events in the table:
Task 1: Find the "number" of Total values for the four events in the table:
• n(M) = the number of males = 60 (Look under the Totals column.)
• n(F) = the number of females = 180 (Look under the Totals column.)
• n(V) = the number of SUVs = 156 (Look under the Totals row.)
• n(C) = the number of Sports Cars = 84 (Look under the Totals row.)

 Task 2: Find the "number" values for specified AND and OR situations from the table:
Task 2: Find the "number" values for specified AND and OR situations from the table:
• n(M and V) = the number of males who prefer SUVs (an intersection of these sets) = 21
• n(F and C) = the number of females who prefer Sports Cars (an intersection of the sets) = 45
Look to where the TWO events intersect with one another - where the column and row intersect.
• n(F or C) = the number of females or preferences of Sports Cars (a union of the sets) = 180 + 84 - 45 = 219
Look for the total of females + the total of Sports Cars, but remember to subtract where these two sets intersect (overlap). In this problem the total number of females choosing a sports car (45) will appear in the total of "all females" and in the total of "all sports cars", thus being counted TWICE. Subtracting ONE of the 45's will give the correct total.

 Task 3: Find the probability that a person chosen at random will be a male who prefers a sport utility vehicle.
Task 3: Find the probability that a person chosen at random will be a male who prefers a sport utility vehicle.
This situation is an AND situation (an intersection):
"the person is a male AND the person prefers a sport utility vehicle"
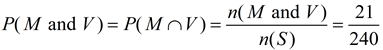
Where n(S) = number in sample space (or the Total of the table).

 Task 4: Find the probability that a person chosen at random will be a female or a person who prefers a sports car.
Task 4: Find the probability that a person chosen at random will be a female or a person who prefers a sports car.
This situation is an OR situation (a union):
"the person is a female OR the person prefers a sports car"
Two formulas are possible for "OR".
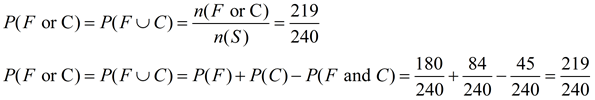

 Task 5: Consider a two way relative frequency table.
Task 5: Consider a two way relative frequency table.
Two Way Whole Table Relative Frequency
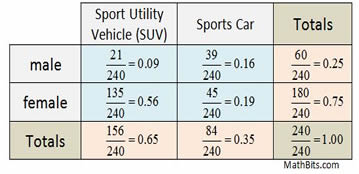 |
You may remember the two way relative frequency table where each entry in the table is divided by a total from the table. When each cell is divided by the table total (in this case 240), you get a two way whole table relative frequency. (There are also row and column relative frequency tables.)
A series of fractions and decimals are created. The decimals may be rounded to two decimal places if needed.
|
These fractions and decimals represent the probability that each cell of the table will occur.
For example, the probability of choosing a male who prefers sports cars is 39/240 or 16%.
The probability of choosing a male is 60/180 = 25%.
While this information is valuable, this table will not yield the probability of more complex situations such those dealing with "OR" situations.