In this section, we will concentrate on examining algebraic cube roots and higher-index roots. Working with these roots are similar to working with square roots, but there are a few additional considerations.
 Let's examine Algebraic Cube Roots: Let's examine Algebraic Cube Roots:
 All Radicals
All Radicals |
Radicals that are simplified have:
1. no fractions left under the radical.
2. no perfect power factors under the radical.
3. no exponents under the radical greater than the index value.
4. no radicals appearing in the denominator of a fractional answer. |
When working with square roots, we searched for factors that occurred in sets of twos.
In cube roots, we are searching for factors that occur in sets of threes.
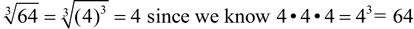
Unlike square roots, consider the following:
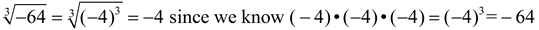
Cube roots are not "bothered" by a negative under the radical symbol.
This is one area where finding a square root and finding a cube root differ.
Cube roots (and any other odd roots) are not concerned with negative values under the radical, because perfect cubes can be negative. Perfect squares (and any other even perfect powers) cannot be negative.
The radical rule below, allows for odd roots to be both positive and negative,
while even roots are always positive.
Before we proceed, take a look at the second table at the right showing algebraic "Perfect Cubes ±". Notice how variables are perfect cubes when their exponents are multiples of three.
To simplify a radical, factor the radicand (under the radical) into factors whose exponents are multiples of the index.
The roots of these factors are written outside the radical, with the leftover factors making up the new radicand. |

 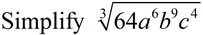
Keep in mind that you are dealing with perfect cubes (not perfect squares). Separate and find the perfect cube factors. A perfect cube can be written as a value times itself three times. Remember, you are looking for values that can be expressed as a power of 3.

 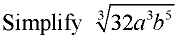
It may be helpful to separate the expression under the radical into separate sections. Be sure to write the cube root (the index 3) for each section. Examine each section for perfect cubes.

|
Perfect Cubes ±
8 = 2 • 2 • 2
27 = 3 • 3 • 3
64 = 4 • 4 • 4
125 = 5 • 5 • 5
216 = 6 • 6 • 6
343 = 7 • 7 • 7
512 = 8 • 8 • 8
729 = 9 • 9 • 9
1000 = 10•10•10
|
Perfect Cubes ±
x3 = x•x•x
x6 = x2•x2•x2
x9 = x3•x3•x3
x12 = x4•x4•x4
Powers are multiples
of 3.
|
Cube Root Notation
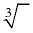

Remember when working with cube roots to ALWAYS write the index value of 3.
|
Remember the Exponent Rules:
xa • xb= xa + b
(xy)b = xb•yb
(xa)b = xab |
Product Rule
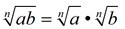 where a and b are real numbers and n is a positive integer where a and b are real numbers and n is a positive integer
"The nth root of a product is equal to the product of the nth roots of each factor."
|
Quotient Rule
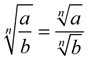
where a and b are real numbers, b not equal to 0, and n is a positive integer
"The nth root of a quotient is equal to the quotient of the nth roots of the numerator and denominator." |
|
 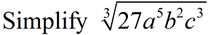
Look for perfect cubes or "hidden" perfect cubes inside of another exponent. The 27 and the c3 are perfect cubes. Yea! The a5 is hiding a perfect cube of a3 • a2. The b2 stands alone since it contains no perfect cubes.


 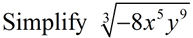
Search out the perfect cubes. Remember that perfect cubes can be negative.


 Let's examine Higher Roots: Let's examine Higher Roots:
Since both a and b are being raised to even powers, we are assured that the radicand is positive, so we can proceed with taking the 4 th root. The absolute value of ab will ensure a positive result.
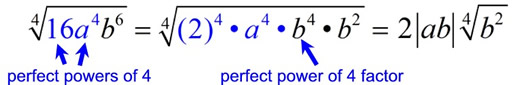

 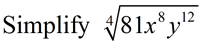
We need to remember that this problem deals with an even root, so the radicand must remain positive. The absolute value of y3 will ensure a positive result.

|