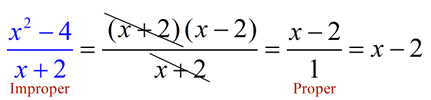Rational numbers are denoted by a script Q.
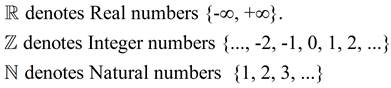
|
|
|
|
A rational number is a number that can be expressed as a fraction p/q where p and q are integers and q ≠ 0. It is the ratio of two integers. |
You are familiar with rational numbers from your work with fractions.
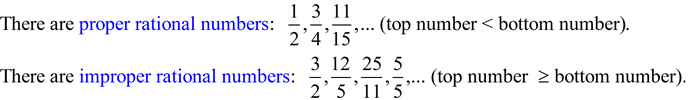

|
A rational expression is an expression that is the ratio of two polynomials. 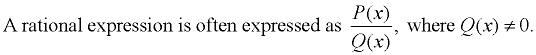
(where P(x) and Q(x) are polynomials) |
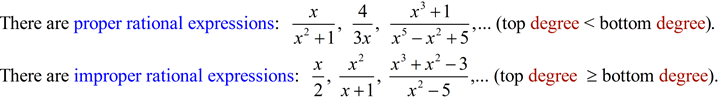
Rational expressions are algebraic fractions in which the numerator is a polynomial and the denominator is also a polynomial (usually different from the numerator). The polynomials used in creating a rational expression may contain one term (monomial), two terms (binomial), three terms (trinomial), and so on.
Rational Expressions
(monomial/monomial) |
Rational Expression
(binomial/binomial) |
Rational Expression
(binomial/trinomial) |
|
|
|
|
Expressions that are not polynomials
cannot be used in the creation of
rational expressions. |
For example: 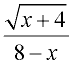 is not a rational expression, since
is not a rational expression, since 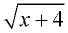 is not a polynomial.
is not a polynomial.

 Since rational expressions represent division, we must be careful to
Since rational expressions represent division, we must be careful to
avoid division by zero (which creates and "undefined" situation).
If a rational fraction has a variable in its denominator, we must ensure that any
value (or values) substituted for that variable will not create a zero denominator.
If it is not obvious which values will cause a division by zero error in a rational expression,
set the denominator equal to zero and solve for the variable.
Examples of "when" rational expressions may be undefined (0 on the bottom):
Rational expression: Could it possibly
be undefined? When? |
Rational expression: Could it possibly
be undefined? When? |
|
Obviously, when x = 1, the denominator will be zero, making the expression undefined.
Domain:All Real numbers but not x = 1. |
|
Set the denominator = 0
and solve.
a2 - 4 = 0
a2 = 4
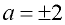 |
For this rational expression, we must limit the x's which
may be used, to avoid a division by zero error, which
leaves the expression undefined.
Notation: 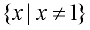 read "all x's such that x ≠ 1." read "all x's such that x ≠ 1."
|
For this rational expression, we must prevent two
x-values from being used in the expression.
Domain: All Real numbers but not a = 2
nor a = -2. 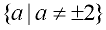 |
Rational expression: Could it possibly
be undefined? When? |
Rational expression: Could it possibly
be undefined? When? |
|
Set: 8 - y = 0
8 = y
Domain: All real numbers, except y = 8. |
|
Set: x2 + x - 12 = 0
(x - 3)(x + 4) = 0
x - 3 = 0; x = 3
x + 4 = 0; x = -4
Domain: All real numbers, but not x = 3 and not x = -4. |
When working with rational expressions,
you may see a statement indicating where the expression will be undefined.
If such information is not stated,
you may be asked to supply this information about the "domain" of the rational expression.

When rational expressions are "improper", division can be used to simplify the expression into a proper form. In Algebra 1, the simplification process limited to determining common factors between the numerator and the denominator was used, as shown below. In Algebra 2, the division component will be explored.