|
Directions: Read carefully.
1. |
Given a1= 5 and an= an-1 + 4, find the explicit formula.
Choose:
|
|
|
2. |
Given an= 3n - 2, find the 19th term.
|
|
|
3. |
Given the sequence:
{5, 7, 9, 11, ...}
a) Which explicit formula generates this sequence?
Choose:
b) Which recursive formula generates this sequence?
Choose:
c) What is the 11th term of the sequence?
Choose:
|
|
|
4. |
There are 80 fish in a Koi pond. Each year the population decreases by 25%. Which explicit formula generates a sequence of fish in the pond each year? |
 |
| |
|
|
5. |
The first four terms of a sequence are:
8, 24, 72, 216, ...
Write a recursive function for this sequence.
Choose:
|
|
|
6. |
A private school purchases $26,400 of new computer equipment. For tax purposes, the school estimates that the equipment decreases in value by the same amount, $3050, each year.
Which explicit function can be used to find the estimated value of the computer equipment?
|
|
Choose:
|
|
|
|
7. |
Given the sequence: 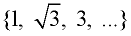
a) Which explicit formula generates this sequence?
Choose:
b) Which recursive formula generates this sequence?
Choose:
c) What is the 5th term of the sequence?
Choose:
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|