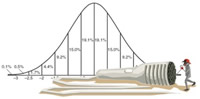
Directions: All questions pertain to normally distributed data. Grab your Z-Score Tables. You can also solve these problems with a graphing calculator.
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||