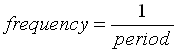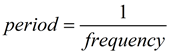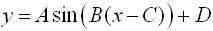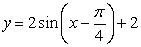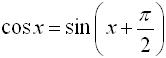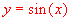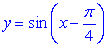|
Let's see what vocabulary is needed to discuss the graphs of trigonometric functions.

 midline: midline: |
|
|
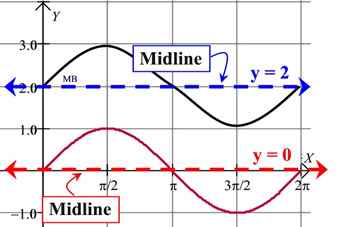
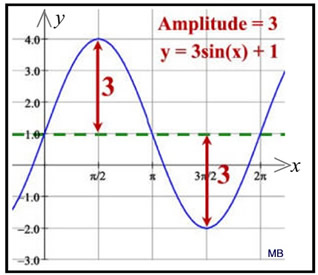
A midline of a sinusoidal function is the horizontal center line about which the function oscillates above and below. For y = sin x, the midline is y = 0 (the x-axis). The midline is parallel to the x-axis and is located half-way between the graphs maximum and minimum values.
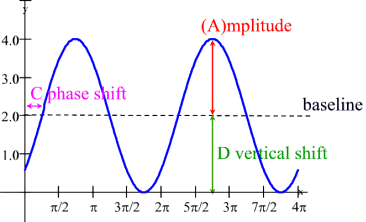
The midline is affected by any vertical translations to the graph. For example, y = sin(x) + 2 has a midline at y = 2.
|
|


 period: period: |
|
|
A periodic function is a trigonometric function which repeats a pattern of y-values at regular intervals. One complete repetition of the pattern is called a cycle. The period of a function is the horizontal length of one complete cycle.
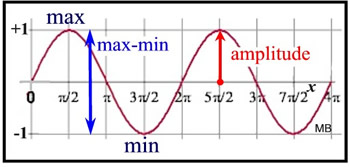
The period may also be described as the distance from one "peak" (max) to the next "peak" (max).
|
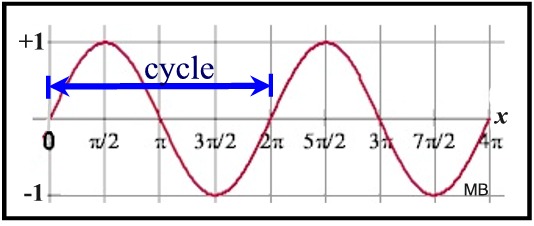
This sine curve, y = sin x, has a period of 2π,
the horizontal length of one complete cycle. |
In functional notation we could say: The period is the smallest value of k in a function f for which there exists some constant k such that f (t) = f (t + k) for every number t in the domain of f.


 sinusoidal curve: sinusoidal curve: |
|
|
A sinusoidal curve is the graph of the sine function in trigonometry.
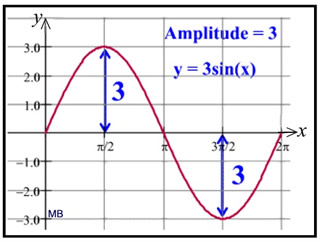
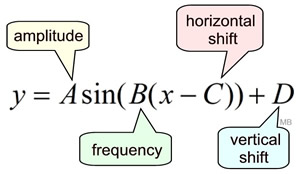
A sinusoid is the name given to any curve that can be written in the form
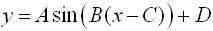
The example at the right is
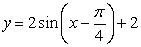 |
|
The cosine wave is also said to be sinusoidal because of the relationship
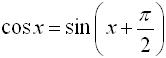
which makes it the sine wave with a
horizontal shift. |
|
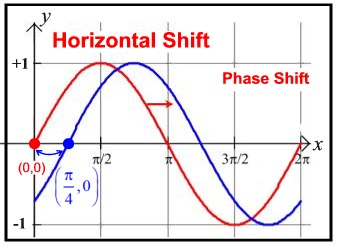
The cosine function, which appears to have a "head start" on the sine function, is often said to lead the sine function (or the sine function lags the cosine function). Both sine and cosine fall under the category of sinusoids, since the cosine graph is simply a 90º shift to the left of the sine graph. The sine and cosine functions are the most popular of the trigonometric functions used for modeling. |

 horizontal shift, phase shift: horizontal shift, phase shift: |
|
|
From the sinusoidal equation,
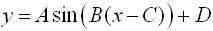
the horizontal shift is obtained by determining the change being made to the x-value.
The horizontal shift is C.
In mathematics, a horizontal shift of a trigonometric function may also be referred to as a phase shift.
(see more about phase shift)
|
|
Remember that the expression (x - C) from the sinusoidal equation, may look like:
• (x - 2) where 2 is a positive value being subtracted, when the shift is to the right.
• (x + 2) where 2 is a negative value being
subtracted, when the shift is to the left. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|