Unit Circle and Trig Graphs MathBitsNotebook.com Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

A unit circle is the source for the generation of the trigonometric function graphs.
The quadrants from the unit circle, when placed horizontally in numerical order, create the basis
for the trigonometric graphs.  This process of creating graphs from the unit circle is often called "unwrapping" the unit circle.

Generate the Sine Function Graph:
Remember that "sine" is represented by the vertical leg of the right triangle positioned in the unit circle as shown below. If these vertical segments, starting at 0º and progressing counterclockwise, are "unwrapped" along a horizontal line, the graph of the sine function is formed.

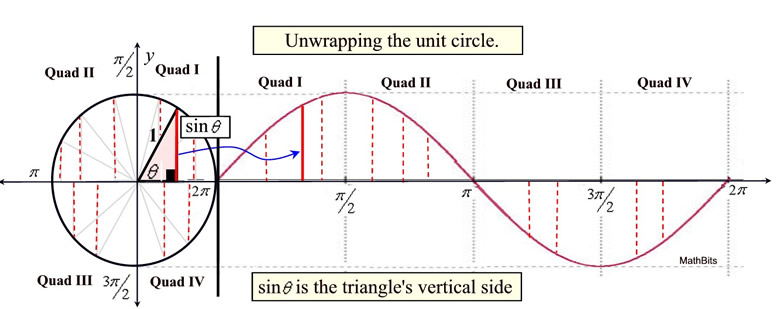
Since the unit circle allows for multiple revolutions, the sine graph will "repeat", which is referred to as being a periodic function. The graph will repeat every period of 2π.
Remember that sine is negative in Quadrants III and IV (the y-coordinates are negative).

Generate the Cosine Function Graph:
Remember that "cosine" is represented by the horizontal leg of the right triangle positioned in the unit circle as shown below. If these horizontal segments, starting at 0º, are progressing counterclockwise, are "unwrapped" along a horizontal line, the graph of the cosine function is formed.

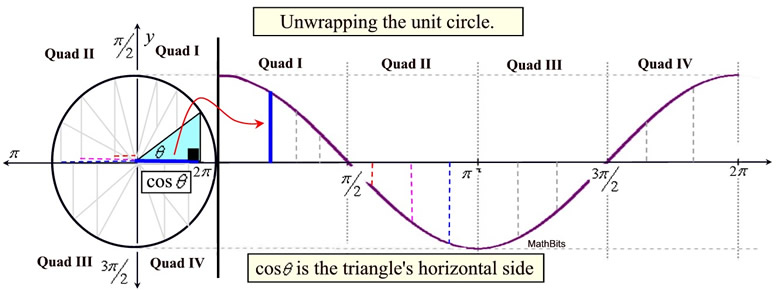
Like the sine graph, the cosine graph will "repeat", making it a periodic function.
The graph will repeat every period of 2π.
Remember that cosine is negative in Quadrants II and III (the x-coordinates are negative).

All of the Trigonometric Functions:
While our efforts will be concentrated on the "unwrapping" of the sine and cosine graphs, as shown above, it is interesting to note that the four remaining trigonometric graphs are formed in a similar manner. Let's take a look at the segments that are used to create the remaining trigonometric graphs.

Each of the six trig functions can be thought of as a segment length related to the unit circle, in a manner similar what was seen for sine and cosine. We have seen that the sine (AF) and cosine (OA) functions are vertical and horizontal segment lengths from a point on the unit circle to the axes. The tangent (BC) and cotangent (ED) functions are the lengths of the line segments tangent to the unit circle from the axis to the terminal ray of angle θ. The secant (OC) and cosecant (OD) functions are the lengths on the rays (or secant lines), from the origin to its intersection with the tangent lines.

Create Graphs from Unit Circle on the Graphing Calculator.

To see how to use your TI-84+ graphing calculator to investigate the unit circle, and create the sine and cosine graphs from the unit circle, follow the link at the right.

For a demonstration of creating the sine and cosine graphs on your calculator, click here.