|
In geometry, it may be necessary to add a line or segment to a diagram to help in solving a problem or proving a concept. Such an added line or segment is called an auxiliary line. The word "auxiliary" means providing additional help or support.
While it is never acceptable to change any of the original parts of a diagram, it is acceptable to add new lines or segments. These new lines are drawn "dashed" or "dotted" to indicated that they were not part of the original diagram.
Auxiliary lines are often used to create a triangle in a diagram or to create two congruent triangles in a diagram. Your goal is to add something to the diagram that will help you solve the problem.
There are a series of postulates that are used to support the addition of an auxiliary line to a proof, such as:
• |
Two points determine one unique line or segment.
|
• |
Each angle has one unique angle bisector. |
• |
Through a point not on a line (segment), only one line can be drawn parallel to the given line (segment). (Parallel Postulate) |
• |
Through a point not on a line (segment), only one line can be drawn perpendicular to the given line (segment). |
• |
Through a point not on a segment, only one line (segment) can be drawn to the midpoint of the given segment. |
Example:
|
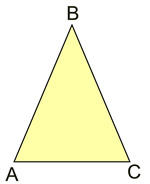
The problem at the left wants us to prove that the base angles of an isosceles triangle are congruent. As you can see, there is not much for us to work with in the diagram. |
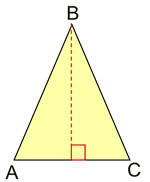 |
The auxiliary segment gives us two triangles with which to work.
|
If we add an auxiliary line which is a perpendicular to the base from point B, we can form two right triangles in which to work. We can then work our way toward getting the angles to be congruent as corresponding parts of congruent triangles. |
Always add an auxiliary line in the simplest way possible. Do not add a multitude of auxiliary lines and make a confusing mess of the diagram.
 Be sure that the conditions that you place on an auxiliary line are actually true. Be sure that the conditions that you place on an auxiliary line are actually true.
Consider this example:
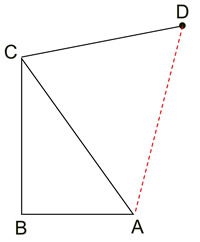 |
Given the diagram at the left, a student draws an auxiliary segment from point D to point A forming a second triangle. The student states that the "Reason" for the auxiliary line is that "through a point not on a line (segment), only one line can be drawn perpendicular to the given line (segment)" and states that 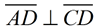 . WRONG!
We have no way of knowing that the perpendicular from A to 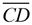 will intersect will intersect 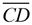 at point D. It will more likely intersect at point D. It will more likely intersect 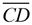 somewhere between point C and point D. The student can draw the segment from A to D, stating that two points determine one unique line, but the student cannot state that the segment is perpendicular to somewhere between point C and point D. The student can draw the segment from A to D, stating that two points determine one unique line, but the student cannot state that the segment is perpendicular to 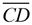 at D. at D. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|