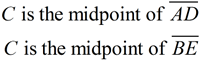The Building Blocks of Proofs

The theoretical aspect of geometry is composed of definitions, postulates, properties and theorems. They are, in essence, the building blocks of the geometric proof. You will see definitions, postulates, properties and theorems used as primary "justifications" appearing in the "Reasons" column of a two-column proof, the text of a paragraph proof or transformational proof, and the remarks in a flow-proof.

divider

A quick review of terms:
• A definition is a precise description of a word used in geometry. All definitions can be written in "if - then" form (in either direction) constituting an "if and only if" format known as a biconditional. See more about definitions at Precision of Definitions.
Example of a definition: An isosceles triangle is a triangle with two congruent sides.
("if - then" form) If a triangle is isosceles, then the triangle has two congruent sides.
(reversed "if-then" form) If a triangle has two congruent sides, then the triangle is isosceles.
("if and only if" form) A triangle is isosceles if and only if the triangle has two congruent sides.

• A postulate is a statement that is assumed to be true without a proof. It is considered to be a statement that is "obviously true". Postulates may be used to prove theorems true. The term "axiom" may also be used to refer to a "background assumption".
Example of a postulate: Through any two points in a plane there is exactly one straight line.

• A theorem is a statement that can be proven to be true based upon postulates and previously proven theorems. A "corollary" is a theorem that is considered to follow from a previous theorem (an off-shoot of the other theorem.) Unlike definitions, theorems may, or may not, be "reversible" when placed in "if - then" form.

Example of a theorem: The measures of the angles of a triangle add to 180 degrees.

• The properties of real numbers help to support these three essential building blocks of a geometric proofs.
Example of a property: A quantity may be substituted for its equal.

divider

Proofs are an Intellectual Game!

A proof is a way to assert that we know a mathematical concept is true. It is a logical argument that establishes the truth of a statement. Lewis Carroll (author of Alice's Adventures in Wonderland and mathematician) once said, "The charm [of mathematics] lies chiefly ... in the absolute certainty of its results; for that is what, beyond all mental treasures, the human intellect craves."

Writing a proof can be challenging, exhilarating, rewarding, and at times frustrating. The building of a proof requires critical thinking, logical reasoning, and disciplined organization. Except in the simplest of cases, proofs allow for individual thought and development. Proofs may use different justifications, be prepared in a different order, or take on different forms. Proofs demonstrate one of the true beauties of mathematics in that they remind us that there may be many ways to arrive at the same conclusion.
 proofguy

Writing a proof is like playing an intellectual game. You have to decide upon which pieces to use for this puzzle and then assemble them to form a "picture" of the situation. Proofs are fun!!

divider

 

Formats for Proofs

The most common form of proof is a direct proof, where the "prove" is shown to be true directly as a result of other geometrical statements and situations that are true. Direct proofs apply what is called deductive reasoning: the reasoning from proven facts using logically valid steps to arrive at a conclusion.

The steps in a proof are built one upon the other. As such, it is important to maintain a chronological order to your presentation of the proof. Like in a game of chess, you must plan ahead so you will know which moves will lead to your victory of proving the statement true. Each statement in your proof must be clearly presented and supported by a definition, postulate, theorem or property. Write your proof so that someone that is not familiar with the problem will easily understand what you are saying.

There are several different formats for presenting proofs. It may be the case, that one particular method of presentation may be more conducive to solving a specific problem than another method.

The Two - Column Proof
Also called the T-Form proof or the Ledger proof.

This proof format is a very popular format seen in most high school textbooks. The proof consists of two columns, where the first column contains a numbered chronological list of steps, called Statements, leading to the desired conclusion. The second column contains the justifications, called Reasons, to support each step in the proof. Remember that justifications are definitions, postulates, theorems and/or properties. This format clearly displays each step in your argument and keeps your ideas organized.

prooftriangle
trianglegiven
Statements
Reasons
divider
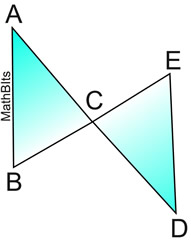
1.
trianglegiven2
vertical line
1.
Given
2.
triproof2
2.
Midpoint of a segment divides the segment into two congruent segments.
3.
triproof3a
3.
Vertical angles are congruent.
4.
triproof4
4.
SAS: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the triangles are congruent.
QED

 

 

The Paragraph Proof

This proof format is a more collegiate method. The proof consists of a detailed paragraph explaining the proof process. The paragraph contains steps and supporting justifications which prove the statement true. When prepared properly, the paragraph can be quite lengthy. When using this method, it can be easy to overlook critical steps and/or supporting reasons if you are not careful. Be sure to list your steps in chronological order, and support each step with a definition, theorem postulate and/or property.

prooftriangle
trianglegiven

It is given that C is the midpoint of both adbe in the supplied figure. Since C is the midpoint, we know that bcde2 because the midpoint of a segment divides the segment into two congruent segments. Knowing vertical angles are congruent, we have angleA. We can now state that Ptriby SAS, because if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the triangles are congruent. QED

 

 

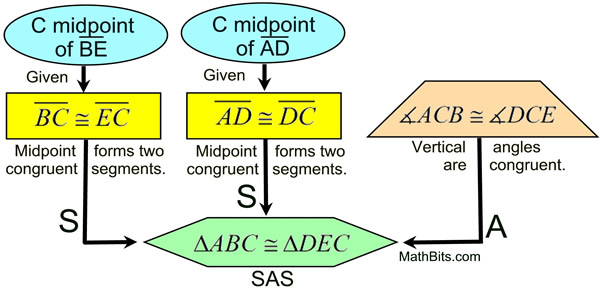
The Flow Proof
Also called the Flowchart Proof.

This proof format shows the structure of a proof using boxes and connecting arrows. The appearance is like a detailed drawing of the proof. The justifications (the definitions, theorems, postulates and properties) are written beside the boxes. The flowchart (schematic) nature of this format resembles the logical development structure often used by computer programmers. This format clearly displays each step in your argument.

prooftriangle
trianglegiven

flow
QED

 

 

Transformational Proof

This proof format describes how the use of rigid transformations (reflections, translations, rotations) can be used to show geometric figures (or parts) to be congruent, or how the use of similarity transformations (reflections, translations, rotations and dilations) can be used to show geometric figures to be similar. The justification in this style of proof will include properties relating to transformations. Be sure you state a sufficient amount of information to thoroughly support your argument. Since transformational proofs are presented in a paragraph format, be sure to organize your ideas in chronological order, and support each idea with a definition, theorem postulate and/or property. We will be highlighting the "ideas" throughout the proof with a "bullet" to make reading the proof easier.
Not all situations will be easily solved by a transformational proof.

prooftriangle
trianglegiven

The basis of this transformational proof will be a rotation of 180º about C.
• A rotation of 180º about C will map A onto cd and map B onto ec since we are dealing with straight segments.
• acbbecause these are the same angle since they have the same sides (rays) and the same vertex.
• abcbecause ∠A'CB' is a 180º rotation of ∠ACB about E, and rotations are rigid transformations which preserve angle measure.
• dceby the transitive property of congruence (or substitution).
• triproof2because a midpoint divides the segment into two congruent segments.
• ca'because a rigid transformation preserves length.
• tritransby SAS.
QED

 

 

Ending a Proof - QED

A traditional method to signify the end of a proof is to include the letters Q.E.D. These letters are an acronym for the Latin expression "quod erat demonstrandum", which means "that which was to be demonstrated".

When a proof is finished, it is time to celebrate your hard work.
Stamp your proof with a QED!


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".