You can draw many different shapes that have four straight sides.
On this page, we will take a look at what we know about four-sided figures, and the information associated with them.
A quadrilateral is basically any figure that has exactly four sides.
A quadrilateral can be any four-sided figure. When we start putting conditions on how the quadrilateral should look, we find that these "special" quadrilaterals fall into categories based upon their characteristics, or properties.
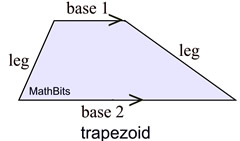
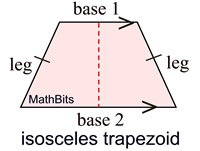
NOTE: This definition is the "inclusive" definition of a trapezoid, meaning that it states "at least one" instead of "exactly one" pair of parallel sides. Under this definition, the word "trapezoid" can apply to quadrilaterals with "one pair" of parallel sides, and also to quadrilaterals with "two pairs" of parallel sides. Most often, you will see the word "trapezoid" associated with quadrilaterals with only one pair of parallel sides, since trapezoids with two pairs of parallel sides have their own distinctive names. First, we will examine trapezoids with one pair of parallel sides. The trapezoids with two pairs of parallel sides will appear under the heading "parallelograms".
Note: The definition of an isosceles triangle states that the triangle has two congruent "sides". But the definition of isosceles trapezoid stated above,
mentions congruent base "angles", not sides (or legs). To find out "Why?", go to the high school Geometry course page.
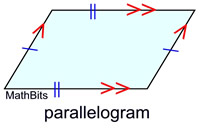
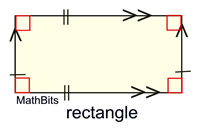
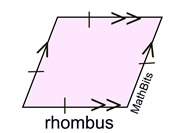
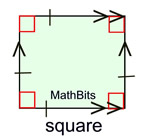
The category of parallelograms will include the "basic" parallelogram along with three additional quadrilaterals that possess ALL of the properties of a parallelogram, plus several additional characteristics of their own. NOTE: At this level, we are concentrating on the shapes of the quadrilaterals and their basic characteristics.
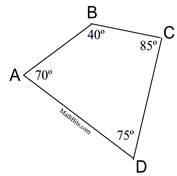
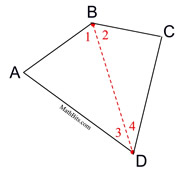
If you draw a diagonal in a four sided figure, you break the figure down (decompose) into two triangles. We know that the sum of the measures of the angles in one triangle is 180º. When the diagonal divides the quadrilateral into two triangles, we can see that the sum of the measures of the angles in the quadrilateral will be the sum of the angle measures from the TWO triangles. The result is a total sum of 360º for the sum of the angles in one quadrilateral.
Topical Outline | JrMath Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
|||||||||||||||||||||||||||||||||||