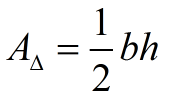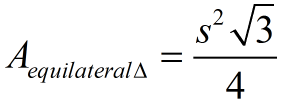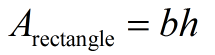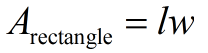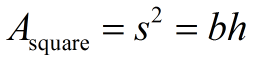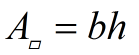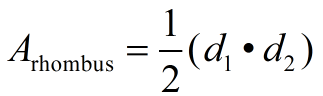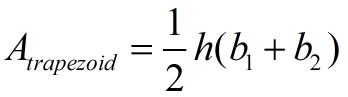|
|
Area is the quantity that expresses the amount of surface a two-dimensional shape covers in square units. |
|
Area is the measure of the surface of a two-dimensional figure.
The area of a shape can be measured by comparing
the shape to squares of a fixed size,
called unit squares.
The unit square can represent different units of measure.
It could be 1 foot by 1 foot.
1 centimeter by 1 centimeter
1 inch by 1 inch, and so on.
|
|
|
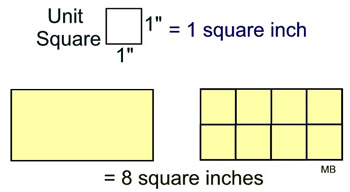
The example at the left shows a rectangle divided into 8 unit squares where each unit square represents 1 square inch.
The area of the rectangle is 8 square inches. |
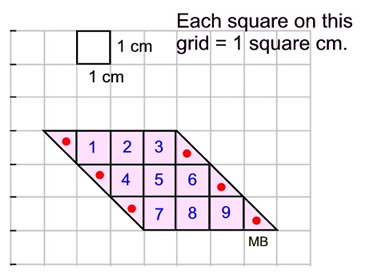
Not all figures can be divided into an exact number of unit squares. Consider the diagram at the right.
A grid, with each square on the grid representing 1 sq. cm., is laid out to show the location of the unit squares.
Six of the unit squares have been cut diagonally, which means cut in half regarding area.
The area of the figures is 9 full unit squares plus 6 half unit squares = 12 square cm. |
|
|
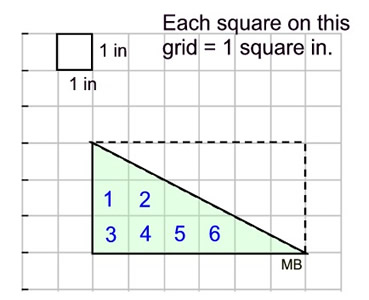
In the diagram at the left, we see 6 full unit squares inside the triangle.
But, we do not know how the other unit squares have been divided. They are not cut along their diagonals which would cut them in half.
Since this is a right triangle, we can create a rectangle around the triangle such that our triangle is half of the rectangle in area.
Area of rectangle = 18 square inches.
Area of triangle = 9 square inches. |
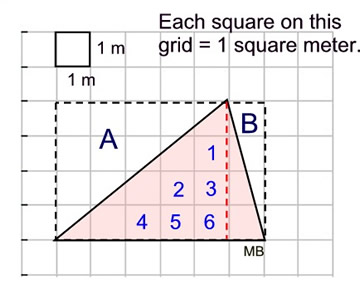
| In the diagram at the right, we see 6 full unit squares inside the triangle.
The triangle in this diagram is not a right triangle, so we cannot simply draw a rectangle around this triangle such that the area of the triangle will be half of the area of the rectangle.
We can, however, in this problem, still draw a rectangle around the triangle to help find the answer. With the addition of the height (red dotted segment), we will have TWO right triangles.
|
|
The left "portion" of the given triangle, along with triangle A, create a rectangle.
Area of left "portion" of given triangle = ½(5)(4) = 10.
The right "portion" of the given triangle along with triangle B, create a rectangle.
Area of right "portion" of given triangle = ½(1)(4) = 2
Total area of triangle: 10 + 2 = 12 square meters
Attempting to count unit squares (as shown above) can become more difficult and confusing as diagrams become more complicated. If the figure is a basic geometric shape, using a "formula" for determining the area may be a better solution strategy.
|
When working with area, you need to know the area formulas
of some basic geometric shapes. You can then use these formulas,
alone or in conjunction with other formulas, to find the area of a figure.
The colored (or painted) surface of the figure represents the area.
Remember to label areas with "square units".
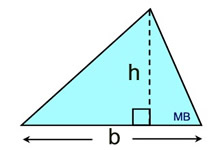b = base and h = height to that base |
Area (all triangles)
|
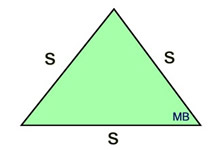s = side length |
*Area (equilateral triangle)
|
* The formula for finding the area of ANY (and ALL) triangles is A = ½bh.
It just so happens that the equilateral triangle also has a
"fancy" formula to find the area if only the lengths of the sides are known. Of course, you can still use the A=½ bh formula on the equilateral triangle.
 The formula you need to memorize for the area of triangles is A = ½bh. |
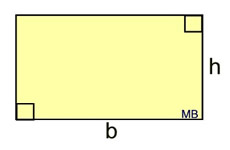b = base and h = height.
(l = length and w = width may also be used) |
Area (rectangle)
|
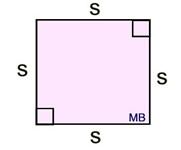s = side length |
Area (square)
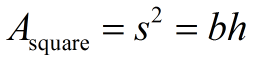A square is a special type of rectangle, so the formula for the area of a rectangle, A = bh, will work just fine for a square.
Just remember, that in the square the b = h. |
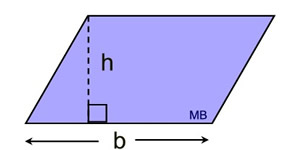b = base and h = height to that base |
Area (parallelogram)
|
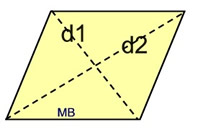d1 = diagonal 1; d2 = diagonal 2 |
*Area (rhombus)
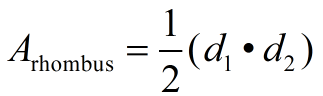The rhombus is a special type of parallelogram, so the formula for the area of the parallelogram, A = bh, will work nicely for the rhombus.
|
* For the "parallelogram group", the area formula, A = bh, will work nicely for all four figures (listed above). The rhombus also has a "fancy" formula for finding the area when you know the diagonals, but the formula A = bh also works for the rhombus.
Regarding the "parallelogram group", the formula you need to memorize
is A = bh, with emphasis on the rectangle and square.
When working with the parallelogram and rhombus, decomposition (cutting the shape up into triangles and rectangles) will be the preferred method, at this level, for finding area. |
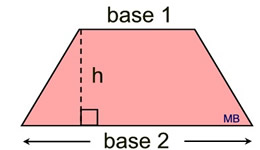base 1 = length of one parallel side
base 2 = length of other parallel side
h = height drawn between the bases |
*Area (trapezoid)
 |
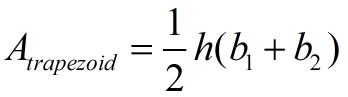| * For the "trapezoids (regular and isosceles)", the preferred method for finding the area, at this level, will be decomposition (cutting the trapezoid up into triangles and rectangles). It may be to your advantage, however, to know the "formula" for the area of a trapezoid, so you can check your calculations. You will need to know this formula in high school mathematics. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
