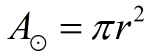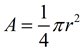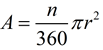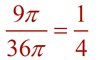|
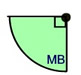
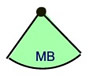
Area of a circle is the area enclosed by a circle. |
|
Area of a circle
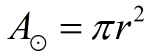 where r = radius of circle
where r = radius of circle
|
|
There is a relationship between the area of a circle and its circumference.
First, remember that the circumference of a circle is C = 2πr,
and the area of a rectangle is A = bh.
A circle can be divided into congruent sectors (pie slices). The sectors are then pulled out of the circle and arranged as shown in the middle diagram. The length across the top (over the curved arcs) is half of the circumference. When placed in these positions, the sectors roughly form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble an actual parallelogram. The parallelogram can be changed into a rectangle by slicing half of the last sector and placing it to the far left. We now have our sectors forming a rectangle.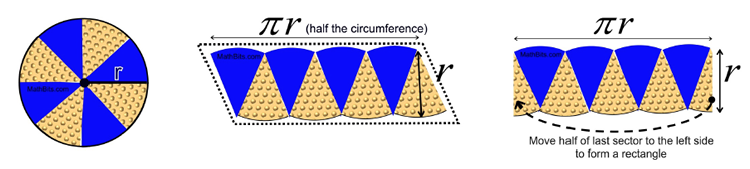
The area of a rectangle is A = bh.
Thus, the area of the sectors that make up the rectangle is πr • r = πr2
The area of a circle: A = πr2


To refresh your memory on expressing answers involving π, see Circumference lesson.

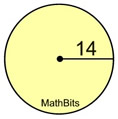
 Find the area of a circle with a radius of 14 inches.
Find the area of a circle with a radius of 14 inches.
Express answer rounded to the nearest hundredth of a square inch.
|
A = πr2
A = πr2 = π(14)2 = 615.7521601 = 615.75
Area = 615.75 square inches |
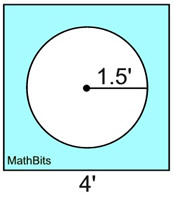
 A square with a side length of 4 feet, has a circle cut out of its interior. The radius of the circle is 1.5 feet. To the nearest square foot, what is the area of the remaining portion of the square?
A square with a side length of 4 feet, has a circle cut out of its interior. The radius of the circle is 1.5 feet. To the nearest square foot, what is the area of the remaining portion of the square?
|
Find the area of the square and subtract the area of the circle.
Area of square = 42 = 16
Area of circle = π(1.5)2 = 7.068583471
16 - 7.068583471 = 8.931416529 = 9 sq.ft.
Answer = 9 square feet |
 Given: two circles with radii of 3 and 6. What is the ratio of the area of the smaller circle to the area of the larger circle?
Given: two circles with radii of 3 and 6. What is the ratio of the area of the smaller circle to the area of the larger circle?
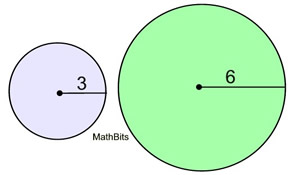 Notice that the ratio of the radii is 1:2, but the ratio of the areas is 1:4. The ratio of the areas is the square of the ratio of the radii.
Notice that the ratio of the radii is 1:2, but the ratio of the areas is 1:4. The ratio of the areas is the square of the ratio of the radii. |
Find the area of each circle.
Since not rounding is mentioned, leave the answer in terms of π.
A(small) = π • 32 = 9π
A(large) =
π • 62 = 36π
Answer: ratio = 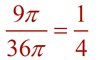
|