|
Directions: Read carefully.
1. |
When it was blown up, this balloon formed a sphere because it was trying to hold as much air as possible with as small a surface as possible.
How much air, to the nearest tenth of a cubic inch, is being held by a spherical balloon with a diameter of 12 inches?
Choose:
|
|
|
2. |
The circumference and height of this right circular cone are shown. Find the volume of this cone, to the nearest cubic foot.
Hint: Use full calculator entries until ready to round the final answer.
Choose:
|
|
|
3. |
A cylinder and a cone each have a radius of 3 cm. and a height of 8 cm. Which of the choices represents the ratio of the volume of the cone to the volume of the cylinder?
Choose:
|
|
|
4. |
A pharmacist is filling medicine capsules. The capsules are cylinders with hemispheres on each end. The length of the cylinder measures 12 mm and the radius is 2 mm. Find, to the nearest tenth, the cubic mm of medication contained in one capsule.
Choose:
|
|
|
5. |
A nursery builds protective cylindrical covers, as shown, to protect seedlings from frost. The cover has a top, but no bottom. How many square feet of flexible plastic will be needed to build three dozen of the covers? The flexible plastic is sold by the square foot.
|
|
| Choose:
|
|
6. |
The official size of a basketball used by the NBA is 29.5 inches in circumference. Which of the following choices expresses the volume of the basketball, to the nearest tenth of a cubic inch?
Hint: Don't round until finished. Use full calculator entries.
Choose:
|
|
|
7. |
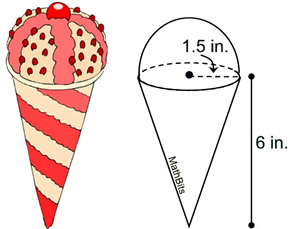
An ice cream cone can be modeled with a right circular cone and a hemisphere. If the ice cream filled the entire cone and the hemisphere, how many cubic inches of ice cream would be needed?
Choose:
|
 |
|
8. |
The radius of a sphere is 4 feet. What is the area of a great circle of this sphere to the nearest square foot ?
Choose:
|
|
|
9. |
A cylinder and a sphere have the same radius and the same height. What is the ratio of the volume of the cylinder to the volume of the sphere?
Choose:
|
|
|
10. |
The cone shown at the right is a right circular cone with a base radius of 8 inches. The cone is sliced parallel to the base. A smaller cone of base radius 4 inches and height of 12 inches is cut off the top. The remaining bottom section of the original cone which is left behind is called a frustum.
Not drawn to scale. |
|
| |
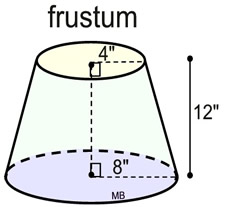 |
a) Find the volume of the frustum. Leave answer in terms of π.
Choose:
|
| |
b) This frustum has the same volume as another right circular cone with a base radius of 8 inches. What is the height, in inches, of this new cone?
Choose:
|
|
11. |
Baked Alaska is a desert made by putting a one inch coating of meringue around a hemisphere of ice cream. The volume of meringue needed in cubic inches, M(r), is given by the formula:
M(r) = 6.14r² + 6.14r + 2.094
where r is the radius of the ice cream in inches.
Find the amount of meringue needed when the radius of the ice cream is 6 inches. Round answer to the nearest cubic inch.
|
|
| Choose:
|
|
12. |
The volume of a sphere is given by the formula: 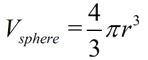
If the volume is given to be 36π cubic inches, what is the radius of the sphere?
Choose:
|
|
|
13. |
This cupcake is made in the shape of a hemisphere. The chocolate cake center is covered with an even layer of marshmallow and sprinkled with pink coconut flakes. If the radius of the chocolate cake center is 1.5 inches and the marshmallow topping is 0.3 inches thick, what is the volume of the marshmallow layer, in cubic inches? |
 The marshmallow layer
The marshmallow layer
does not cover the base.
Round answer to the
nearest tenth of a cubic inch.
|
| |
Choose:
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|