|
|
 |
Linear equations are equations of degree one.
(The variable has an exponent of one.)
|
Solving equations is a process of undoing operations (such as +, -. ×, ÷) that are affecting the variable. The goal is to isolate the variable (get it alone) on one side of the equal sign.
|
Linear equation: x + 8 = 18
Goal: Get the variable, x, ALONE on one side of the equal sign.
Remember that the "equal sign" implies that the expressions on either side are equivalent. You can think of both expressions as "weighing" the same amount. You must be careful, when solving for the variable, to maintain an equal "weight" on both sides. This process of "balancing the equation" is accomplished by always making the same changes to BOTH sides of the equal sign.
In simple equations, you may only need to "undo" one operation to solve the equation, thus the reference to "one-step" equations. |
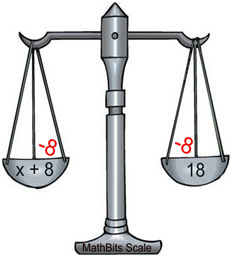 x + 8 = 18 x + 8 = 18
Subtract x from both sides. x = 10.
|
|
 Solving one-step equations: (undo operation by either add or subtract) Solving one-step equations: (undo operation by either add or subtract)
Solve for x: x - 7 = 12 |
|
Analysis: We need to isolate the variable x.
Since the number 7 has been subtracted from x, we will need to do the opposite and add 7, to get rid of the -7.
This process is actually using the additive inverse property to create a 0 on the left side (-7 + 7 = 0), and then using the additive identity to isolate the x, since x - 0 = x. |
|
 |
Remember to add the 7 to BOTH sides of the equation, to keep the equation balanced. |
|
Check answer: A nice bonus to solving equations is that you always know if you have the correct answer. Simply substitute your answer into the original equation and see if the result is true. |
Check:
x - 7 = 12
19 - 7 = 12
12 = 12 True!
|
|
Note: The variable can be located on either side of the equal sign.
[ x = 19 and 19 = x are saying the same thing. Both are the correct answer. ]
It is customary to write the variable on the left, like x = 19, simply because it "reads" better.
Solve for x: x + 6 = 9 |
|
Analysis: We need to isolate the variable x.
Since the number 6 has been added to x, we will need to do the opposite and subtract 6, to get rid of the 6.
This process is actually using the additive inverse property to create a 0 on the left side (6 - 6 = 0), and then using the additive identity to isolate the x, since x + 0 = x. |
|
 |
Remember to subtract 6 from BOTH sides of the equation, to keep the equation balanced. |
|
Check answer: Substitute your answer into the original equation and see if the result is true. |
Check:
x + 6 = 9
3 + 6 = 9
9 = 9 True!
|
|

 Solving one-step equations: (undo operation by multiply, or divide by non-zero) Solving one-step equations: (undo operation by multiply, or divide by non-zero)
Solve for x: 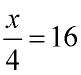 |
|
Analysis: We need to isolate the variable x.
Since x has been divided by 4, we will need to do the opposite and multiply by 4, to get rid of the 4.
This process is actually using the multiplicative inverse property to create a 1, and then using the multiplicative identity to isolate the x, since 1•x = x.
This problem could also be solved by dividing both sides by 1/4 (which is the same as multiplying by 4). But, why make the problem more difficult! |
|
 |
Remember to multiply BOTH sides of the equation by 4, to keep the equation balanced. |
|
Check answer: Substitute your answer into the original equation and see if the result is true. |
Check:
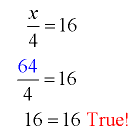
|
|
Solve for x: 5x = 125 |
|
Analysis: We need to isolate the variable x.
Since the number 5 has been multiplied times x, we will need to do the opposite and divide by 5, to get rid of the 5.
This process is actually using the multiplicative inverse property to create a 1, and then using the multiplicative identity to isolate the x, since 1•x = x.
This problem can also be solved by multiplying both sides by 1/5 (which is the same as dividing by 5). |
|
 |
Remember to divide BOTH sides of the equation by 5, to keep the equation balanced. |
|
Check answer: Substitute your answer into the original equation and see if the result is true. |
Check:
5x = 125
5(25) = 125
125 = 125 True!
|
|

 Solving one-step equations: (containing fractions or decimals) Solving one-step equations: (containing fractions or decimals)
The same strategies shown above can be used to solve one-step equations containing fractions or decimals. The fraction, or decimal, may appear as a constant term or as the coefficient of the variable.
Solve for x: x + 4.5 = 9.9 |
|
Analysis: Isolate the variable.
Strategy: subtract 4.5 from both sides.
Check:
5.4 + 4.5 - 9.9
9.9 = 9.9 True!
|
|
Solve for x:  |
|
Analysis: Isolate the variable.
Strategy: divide both sides by 9
Check:
 . .
|
|
Solve for x: 1.2x = 4.8 |
|
Analysis: Isolate the variable.
Strategy: divide both sides by 1.2.
Check:
1.2(4) - 4.8
4.8 = 4.8 True!
|
|


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|



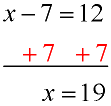
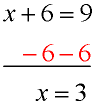
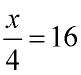
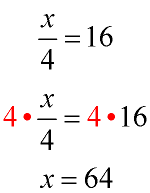
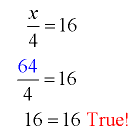

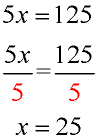


 .
.

