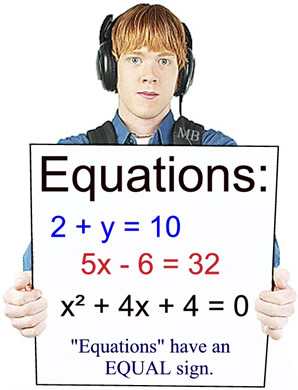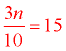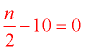|
 Algebraic Equations: Algebraic Equations:
In the previous unit lesson Translating Expressions, we worked with some of the most common words and phrases used in translating algebraic expressions.
|
add
sum
more than
increased by
exceeds
in all
combined
total
gain
plus
deposit |
subtract
difference
less than
decreased by
diminished by
minus
fewer
reduced by
take away
withdraw |
multiplied by
of
product
times
double
twice
triple
|
divide
quotient
divided equally
per
ratio of
split into
fraction |
"Expressions" and "equations" refer to two different entities in mathematics.
If you are dealing with an "equal sign", you are dealing with an "equation".
Unlike expressions, algebraic equations contain an equal sign.
EQUAtion  EQUAL sign EQUAL sign
An equation is a sentence where two algebraic expressions are equal.
To our list of "words"
as shown in the chart at the top of this page,
we can now add a sampling of words that imply the need of "an equal sign".
EQUAL |
is,
are, was, were, equivalent to, same as, yields, gives |
Also, continue to look for commas, to help you group your terms.
|
If you are having trouble determining what the equation might be, make up a numerical problem to see how the numbers in the problem are related to one another.
|
 |
Translate the following verbal problems into equations, |
| |
Verbal Statement |
Algebraic Equation |
1. |
Three times a number, divided by ten equals fifteen. |
|
2. |
Ten less than the quotient of a number and two is zero. |
|
3. |
Twelve more than the product of a number and two is thirty-six. |
2n + 12 = 36 |
4. |
Represent the cost of access to a movie web site which charges a $5 fee for the first month, and then $28 a month for continued access after the first month.
Numerical Example: For 4 months the cost would be: Cost = $5 + $28•(4-1). Replace 4 with m for number of months. |
c = cost, m = months
c =
5 + 28(m - 1) |
5. |
If chocolate doughnuts cost $1.50 and chocolate chip muffins cost $2.25, how many of each can you purchase for $20?
Numerical Example: The cost of 3 doughnuts and 2 muffins will be: Cost = $1.50•3 + $2.25• 2. Replace 3 with d for dough-nuts, 2 with m for muffins, and Cost with $20.
|
d =doughnuts, m = muffins
20 =
1.50d + 2.25m |
6. |
Express the area of a rectangle whose length is twice its width decreased by 6.
Numerical Example: If the width is 10, the length is 14, then the area, A = 10 • 14. Just replace 10 with w for width, and 14 with 2w - 6 for the length. |
A = area, w = width
A = w • (2w - 6) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|