|
|
A polygon is a 2-dimensional closed figure that is the union of line segments in a plane. A polygon has three or more sides. |
|
You already have a good understanding of 3-sided and 4-sided polygons from your previous studies of geometry.
3-sided polygons - triangles - all types
(acute, right, obtuse, equiangular, scalene, isosceles, equilateral)
4-sided polygons - quadrilaterals - all types
(kite, rhombus, square, trapezoid, parallelogram, rectangle)
We will now enhance these previous concepts
and add some new information.
|
 |
Classifications of Polygons |
 Polygons can be classified as either regular or irregular (not regular).
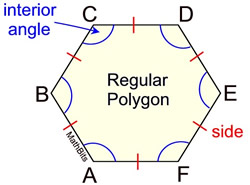
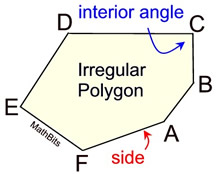
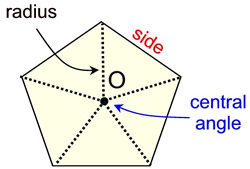
You have already been working with some regular polygons.
A regular triangle is an equilateral
triangle (also called an equiangular triangle).
All of its sides are the same length.
All of its angles are the same measure (60º).
|
A regular quadrilateral is a square.
All of its sides are the same length.
All of its angles are the same measure (90º).
|
|
A regular polygon is a polygon in which all of the sides are of equal length and all of the angles are of equal measure.
It is both equilateral and equiangular. |
|
Now, extend this concept to figures with more than four sides:
In a regular polygon, all of its interior angles are of the same measure and all of its sides are the same length.
A regular 6-sided polygon.
A " regular hexagon". |
In an irregular polygon, the interior angles may be of different measures and the sides may be different lengths.
An irregular 6-sided polygon
A "hexagon ". |
 |
The term "polygon" refers to a type of figure which may be regular or irregular. Do NOT assume "polygon" means "regular polygon". If a polygon is a regular polygon, it will be stated as such. |
Polygons can be classified as either convex or concave.
A polygon is convex if no line that contains a side of the polygon contains a point in the interior of the polygon. In a convex polygon, each interior angle measures less than 180 degrees. A triangle is always convex, and regular polygons are always convex.
Concave polygons "cave-in" to their interiors, creating at least one interior angle greater than 180 degrees (a reflex angle).
|
|
Parts of Regular Polygons |
Regular Pentagon
 |
The center, (O), of a regular polygon, is a point in the interior of the polygon equidistant from each vertex. It is also the center of the inscribed and circumscribed circles. The radius is the distance from the center to any vertex.
The central angle of a regular polygon is formed by connecting the center to two adjacent vertices. All central angles are of equal measure in a regular polygon. |
Irregular polygons are not described as having a "center" which is equidistant from each vertex. As such, an irregular polygon does not have central angles or radii. An irregular polygon does, however, have a center of gravity, called a centroid. |
The table below shows some of the more commonly used polygons.
Do NOT assume that the diagrams in the "Figure" column are "regular" polygons.
Polygon |
Figure |
Sides |
Angles |
Diagonals |
Number
Triangles |
Triangle |
|
3 |
3 |
0 |
1 |
Quadrilateral |
|
4 |
4 |
2 |
2 |
Pentagon |
|
5 |
5 |
5 |
3 |
Hexagon |
|
6 |
6 |
9 |
4 |
Heptagon or Septagon |
|
7 |
7 |
14 |
5 |
Octagon |
|
8 |
8 |
20 |
6 |
Nonagon or Novagon |
|
9 |
9 |
27 |
7 |
Decagon |
|
10 |
10 |
35 |
8 |
Dodecagon |
|
12 |
12 |
54 |
10 |
n-gon |
---- |
n |
n |
½n(n - 3) |
(n - 2) |
An n-gon is a polygon with n sides.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
