Regarding the Set of Real Numbers:
 We have already noticed that the Commutative and Associative Properties of Real Numbers, while applying to addition and multiplication, do NOT apply to subtraction nor division. We have already noticed that the Commutative and Associative Properties of Real Numbers, while applying to addition and multiplication, do NOT apply to subtraction nor division.
Even the titles of these properties specify "of addition" or "of multiplication".
| |
The Commutative and Associative Properties do NOT WORK for subtraction or division.
|
 |
Subtraction: |
5 - 2 ≠ 2 - 5 [3 ≠ -3] |
Not Commutative. |
| |
7 - (4 - 3) ≠ (7 - 4) - 3 [6 ≠ 0]
|
Not Associative. |
|
|
|
Division: |
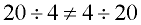 [5 ≠ 1/5] [5 ≠ 1/5] |
Not Commutative. |
| |
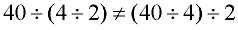 [20 ≠ 5] [20 ≠ 5] |
Not Associative. |
 The Closure Property of Real Numbers also has specifications stating "of addition" or "of multiplication". Does this mean that there are difficulties with closure of the real numbers under "subtraction" and "division"?
Not quite! The Closure Property of Real Numbers also has specifications stating "of addition" or "of multiplication". Does this mean that there are difficulties with closure of the real numbers under "subtraction" and "division"?
Not quite!
Subtraction: |
9 - 4 = 5; |
17 - 20 = -3 |
Subtracting two real numbers (which is really adding its opposite) creates another real number. Real numbers are closed under subtraction. |
| |
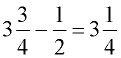 ; ; |
3.5 - 0.8 = 2.7 |
|
|
|
Division: |
20 ÷ 5 = 4; |
1.5 ÷ 3 = 0.5 |
The division of nearly all real values will produce another real number.
BUT, because division by zero is undefined (not a real number), the real numbers are NOT technically closed under division. |
| |
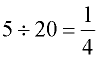 ; ;
|
|
BUT 3 ÷ 0 = undefined |
Note: Some textbooks state that " the real numbers are closed under non-zero division" which, of course, is true. This statement, however, is not equivalent to the general statement that "the real numbers are closed under division". Always read carefully!
Remember: To say that a set of values is closed under a specific operation,
the set must be closed for ALL of its values under that operation.
Regarding Other Sets of Numbers:
If we examine some of the subsets of the Real Numbers as independent sets, we run into some interesting situations regarding subtraction and division. Let's see what does, and does NOT, work with the set of counting numbers, the set of integers, and the set of rationals:
| |
The set of Counting Numbers (Natural Numbers) {1, 2, 3, 4, ... }
|
Commutative (subtraction) |
Nope! |
5 - 3 ≠ 3 - 5 |
Commutative (division) |
Nope! |
10 ÷ 2 ≠ 2 ÷ 10 |
Associative (subtraction) |
Nope! |
2 - (5 - 6) ≠ (2 - 5) - 6 |
Associative (division) |
Nope! |
6 ÷ (3 ÷ 2) ≠ (6 ÷ 3) ÷ 2 |
Closure (subtraction) |
Nope! |
4 - 7 = -3 (no negative counting numbers) |
| |
Closure (division) |
Nope! |
4 ÷ 8 = ½ (no fractions in counting numbers) |
| |
The set of Integers {..., -3, -2, -1, 0, 1, 2, 3, ... }
|
Commutative (subtraction) |
Nope! |
(-4) - 3 ≠ 3 - (-4) |
Commutative (division) |
Nope! |
9 ÷ (-3) ≠ (-3) ÷ 9 |
Associative (subtraction) |
Nope! |
3 - (4 - (-5)) ≠ (3 - 4) - (-5) |
Associative (division) |
Nope! |
-6 ÷ (3 ÷ 2) ≠ (-6 ÷ 3) ÷ 2 |
Closure (subtraction) |
Good! |
-8 - (-3) = -5 |
| |
Closure (division) |
Nope! |
4 ÷ 8 = ½ (no fractions in the integers)
Also, division by zero is a problem. |
| |
The set of Rationals (a number that can be expressed as p/q, integers p,q, q≠0) |
Commutative (subtraction) |
Nope! |
5½ - 3 ≠ 3 - 5½ |
Commutative (division) |
Nope! |
10 ÷ 2 ≠ 2 ÷ 10 |
Associative (subtraction) |
Nope! |
2½ - (5 - 6) ≠ (2½ - 5) - 6 |
Associative (division) |
Nope! |
6 ÷ (3 ÷ 2) ≠ (6 ÷ 3) ÷ 2 |
| |
Closure (subtraction) |
Good! |
8/3 - 4/1 = -4/3 |
| |
Closure (division) |
Nope! |
5 ÷ 0 = undefined (not a rational number) |
| |
|
Remember: 0 itself is a rational number (0 = 0/1).
So 5 ÷ 0 is a "rational being divided by a rational".
But the result violates the definition of rational form [ p/q where q ≠ 0 ]. |
|