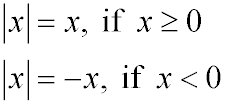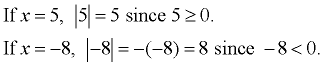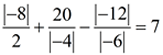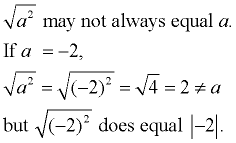Note: This unit will discuss "absolute value" as it relates to real numbers.
Keep in mind that the absolute value of a complex number, z = a + bi,
is written as | z | or | a + bi |. It is a non-negative real number defined as:
, the distance from 0 in the complex plane.
Refer to Complex Numbers.




The absolute value (or modulus) of a real number. | x |, is the
non-negative magnitude of x measured without regard to its sign.

The absolute value of a number is the distance between the number and zero
on the real number line.

Distances are measured as positive units (or zero units).
Consequently, absolute value is never negative.

Absolute value answers the question "How far from zero?",
but not the question "In which direction from zero?".


The notation used for absolute value is two vertical bars.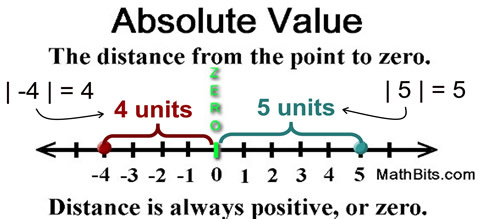

absgraphMBRB

statement
Algebraically speaking,

Abs Rule

While it is understood that absolute value yields a positive result (or zero), you must be a bit more careful when stating this concept using a variable, such as x. One never knows the value which may replace the variable (such as x) as it could be positive, or it could be negative.

If x = 5,   | 5 | = 5,   since 5 > 0.
If x = -8,   | -8 | = - (-8) = 8.   since -8 < 0.


bullet Examples:
1.  | − 3 | = 3
2.   − | − 7 | = − 7
 
3.   | 0 | = 0
4.   | − 5 |2 = 25
 
5.   − | (− 8)2 | = − 64
6.   − | − 3 |2 = − 9
 
7.   | 3 | + | − 7 | − | − 2 | = 8
8.   | − 8 | + ( − 9) + | − 14 | + ( − 2) = 11
 
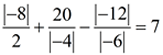9.  absex12
10.  | − 3 + 6 |2 + | − 3 | = 12


bullet Things to Consider:
Measuring Distance:
| 8 − 3 | = 5  and   | 3 − 8 | = 5

The expression | a − b | represents the distance from
a to b on the number line.

This distance is the same when measured forward from 3 to 8, or backward from
8 to 3.

Properties:
| 3 • 7 | = | 3 | • | 7 |

1. | a • b | = | a | • | b | (multiply)
2. | a / b | = | a | / | b | (divide)
3. | a + b | ≠ | a | + | b | (add)
4. | a - b | ≠ | a | - | b | (subtract)
5. | an | = | a |n (power)
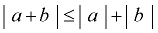6. abstrineq(called the Triangle Inequality)
Square Root Definition:

abssqrtdef
The absolute value sign is needed.
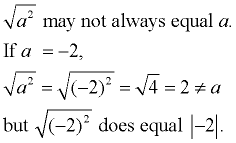squareroot2a



bullet Graph:
 

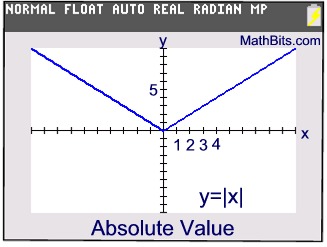
Since absolute value always yields a positive result, or zero, the graph of absolute value plots only y-values that are positive, or zero.

The graph resides above the x-axis (plus the origin), in quadrants I and II.

y = | x |    arrow





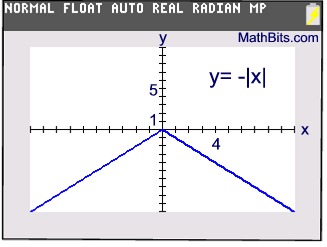Negating absolute value creates y-values that
are negative or zero. The graph resides in
quadrants III and IV (plus the origin).

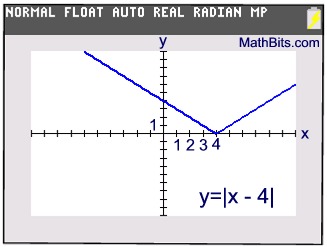Subtracting 4 from x moves the absolute value
graph horizontally 4 units to the right. The
y-values remain positive or zero.




For help wotj absolute value
on your
calculator.
click here.
ti84c
For help with absolute value
 on your
calculator,
click here.

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".