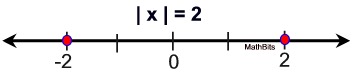Solving an absolute value inequality is similar to solving an absolute value equation,
with a few more considerations. When dealing with inequalities, you will be dealing with more possible values as solutions. Check out the following comparisons:

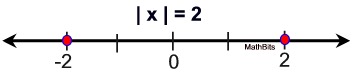
ineqgraph3

LESS THAN: GREATER THAN:
| x | < 2

ineqgraph1
x > -2   and    x < 2
also written: -2 < x < 2
| x - 0 | < 2 represents the distance between x and 0 that is less than 2. The solution will be all of the values on the number line between -2 and +2.
| x | > 2

ineqgraph2
x < -2   or    x > 2
| x - 0 | > 2 represents the distance between x and 0 that is greater than 2. The solution will be all of the values on the number line to the right of +2 and those to the left of -2.
LESS THAN OR EQUAL TO: GREATER THAN OR EQUAL TO:
| x | < 2
ineqgraph1
x > -2   and    x < 2
also written: -2 < x < 2
| x | > 2
ineqgraph2
x < -2   or    x > 2

Now, let's formalize these observations into a more mathematical statement:

Absolute Value Inequalities:
If the symbol is < (or <):     (and)
If a > 0, then the solutions to | x | < a
are x < a   and   x > -a.
Also written:   -a < x < a
If a < 0, there is no solution to | x | < a.
Think about it: absolute value is always positive (or zero), so, of course, it cannot be less than a negative number.

If the symbol is > (or >):     (or)
If a > 0, then the solutions to | x | > a
are x > a   or   x < -a. 
If a < 0, all real numbers will satisfy | x | > a.
Think about it: absolute value is always positive (or zero), so, of course, it is greater than any negative number..

ti84c
For help with solving absolute value inequalities
 on your calculator,
click here.
Keep in mind that your graphing calculator can be used to solve absolute value inequalities and/or double check your answers.

dividerdash


ex1 Solve for x:  | x - 3 | < 4        [Working with "less than or equal to"]
Case 1:
x - 3 < 4
x < 7
and
Case 2:
x - 3 > -4
x > -1
Note that there are two parts to the solution and that the connecting word is "and".
Solution:  x > -1 and x < 7
also written as:    -1 < x < 7


dividerdash



Solve for x:    | x - 20 | > 5            [Working with "greater than"]
Case 1:
x - 20 > 5
x > 25
or
Case 2:
x - 20 < -5
x < 15
Note that there are two parts to the solution and that the connecting word is "or".
Solution:  x < 15 or x > 25


dividerdash

ex3 Solve for x:  | 3 + x | - 4 < 0              [Isolate absolute value.]
Case 1:
| 3 + x | < 4
3 + x < 4
x < 1
or
Case 2:
| 3 + x | < 4
3 + x > -4
x > -7
Note that the absolute value is isolated before the solution begins.
Solution:  x < 1 and x > -7
also written as:    -7 < x < 1


dividerdash

ex4 Solve for x:  5 < | x + 1 | < 7              [compound inequality]

Separate a compound inequality into two separate problems.
5 < | x + 1 |
| x + 1 | < 7
Case 1:
5 < x + 1
4 < x
or
Case 2:
-5 > x + 1
-6 > x
Case 1:
x + 1 < 7
x < 6
and
Case 2:
x + 1 < -7
x > -8
Solution:  x > 4 or x < -6
Solution:  -8 < x < 6

Now, find where the solutions overlap!
numline2

Solution:  -8 < x < -6   as well as    4 < x < 6


dividerdash

ex5 Solve for x:  | x + 4 | > -3                        [All values work.]
Case 1:
x + 4 > -3
x > -7
or
Case 2:
x + 4 < 3
x < -1
whoa
You already know the answer!
Absolute value is always positive (or zero),
so it is always > -3.
All values work!
Solution:  x > -7 or x < -1
er


dividerdash

Solve for x:  | x + 1 | < -6                        [No values work.]
Case 1:
x + 1 < -6
x < -7
and
Case 2:
x + 1 > 6
x > 5
whoa
You already know the answer!
Absolute value is always positive (or zero).
It is NEVER < -6.
No values work!
Solution:  x < -7 and x > 5 ??
The answer is the empty set Ø.


dividerdash

ex7 [word problem]
It is reported that the average yearly salary for computer programmers in the United States is $51,423 per year, but can vary depending upon location. The actual salary could differ from the average by as much as $15,559 per year.
a) Write an absolute value inequality to describe this situation.
b) Solve the inequality to find the range of the starting salaries.

Solution:
Remember that | x - a | < b represents the set of all points that are less than b units
away from a.

a) | x - 51423 | < 15559
    | the difference between the average and the salary | < $15,559

b)
Case 1:
| x - 51423 | < 15559
x - 51423 < 15559
x < 66982
Case 2:
| x - 51423 | < 15559
x - 51423 > -15559
x > 35864

Answer: $35,864 < x < $66,982
The absolute value inequality verifies what common sense tells you the answer to be.




divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".