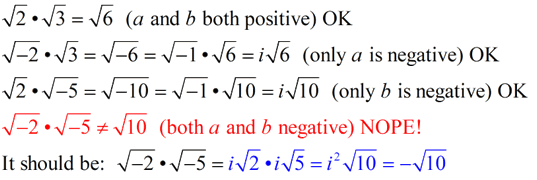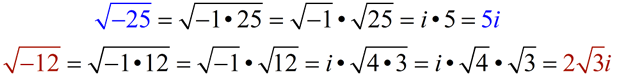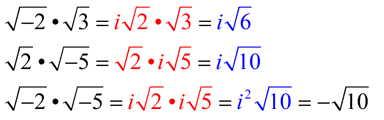|
You discovered, during your study of quadratic equations in Algebra 1, the existence of square roots of negative numbers. Such square roots are called "imaginary numbers".
See the Refresher page.
|
The imaginary unit, i, is the number whose square is negative one.
|
i 2 = -1 |
|
|
i 2 = -1 and 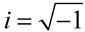
The imaginary unit i possess the unique property that when squared, the result is a negative value.
Consequently, when simplifying the square root of a negative number, an "i " becomes part of the answer.
|
Product Rule(s) for Square Roots
|
Up to this point, our work with square roots and Real numbers has involved only positive values under the radical. Thus, our Product Rule for Square Roots dealt only with positive Real number values.
|
Product Rule
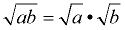
where a ≥ 0, b≥ 0 |
|
But, when working with imaginary numbers, we need to extend our Product Rule for Square Roots to allow for ONE negative value under the radical.
Either "a" is negative OR "b" is negative, but NOT BOTH!
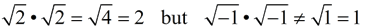

|
Product Rule
(extended)
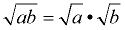
where a ≥ 0, b≥ 0
OR a ≥ 0, b < 0
but
NOT a < 0, b < 0 |
|
Keep in mind that the Product Rule for Square Roots is saying that when multiplying two separate square roots, the solution will be the square root of the product of the two separate radicands.
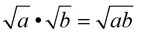
Notice the problem that develops if this rule is followed as written:
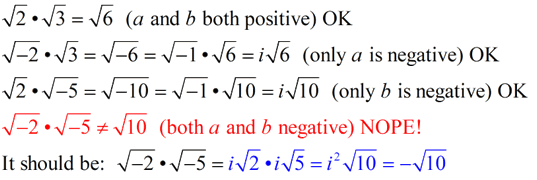
To avoid this problem, always deal with the i-part first, as shown in blue above.
|
|
The secret to dealing with the square root of a negative value
is to deal with the i-part first! |
|
Pull out the factor of -1 first, and then simplify the remaining portion of the square root.
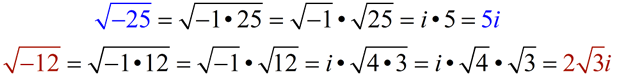
Be careful when you hand write your answer that "i " does not appear to be "under" the radical symbol.
You will often see answers written with the "i " in front of the radical to avoid this problem.
Pulling out the "i " from the square root of a negative value first is always the best plan.
Writing the "i " in front of the radical is a good plan so there is no confusion in your answer.
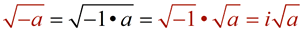 (where a≥ 0) (where a≥ 0)
Check out a better way to write the product statements from the green box above:
Pulling out the "i " first. Writing "i " in front of radical.
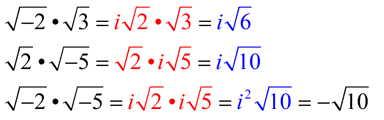

|
An imaginary number, is any number that contains the imaginary unit, i. It takes the form of a + bi where a and b are real numbers, but b ≠ 0. |
Examples: 3 i, -5 i, πi, 6 + 3 i, -2 - 4 i, 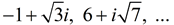
When a = 0, the number may be referred to as purely imaginary, such as 3 i, -5 i, and πi. |
|
When you put the Real Numbers together with the Imaginary Numbers,
you get the set of Complex Numbers.
|
A complex number is a combination of a Real Number and an Imaginary Number, written as a + bi (where a and/or b may equal zero).
(a and b are real numbers and i is the imaginary unit)
|
|
• If we have a + bi with a = 0, we have 0 + bi which gives bi, a purely imaginary number.
• If we have a + bi with b = 0, we have a + 0i which gives a, a real number. |
In this manner, we can see that real numbers and imaginary numbers are also complex numbers.
In " a + bi ", the real number
" a" is referred to as the "real part" of the complex number and
" bi" (where b is a real number) is referred to as the "imaginary part" of the complex number.
The " b" is
referenced as the number of multiples of i.
Real Numbers: 3, 0, 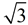 , 0.125, π, -42.1, e, ... , 0.125, π, -42.1, e, ... |
 |
Complex Numbers: 2 + 3i, -3 - i ,
8 + 0i, 0 + 4i, 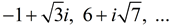
(Includes All Reals and All Imaginaries)
|
| Imaginary Numbers: i, -3i, 2i, πi, -5.1i, ... |
| Complex numbers are generally referenced by the letter "z" such as z = a + bi. |
 Clarification on vocabulary: Clarification on vocabulary:
pure imaginary number
"bi "
A pure imaginary number can be written in bi form where b is a non-zero real number and i is the imaginary i.
Examples: 3i, -6i,  , ,  |
complex number
"a + bi "
A complex number may appear as any real number a, a pure imaginary number bi, or the sum of both.
Examples: 8 (which is 8 + 0i), 6i (which is
0 + 6i), 3 + 9i, -2 - 5i,
|
The set of real numbers and the set of imaginary numbers are subsets of the set of complex numbers. |
All Real Numbers are Complex Numbers!
The set of Complex Numbers is the "Big Guy" for "numbers",
as it contains ALL of the possible sets of numbers.
|
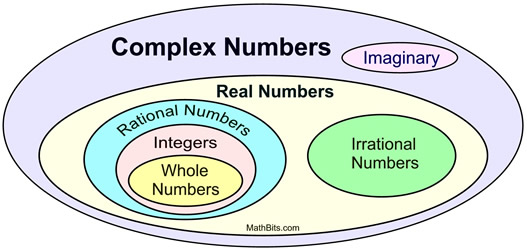
From Algebra 1, we know that the Real Numbers are composed of two main subsets,
the "Rational Numbers" and the "Irrational Numbers".
Now, we know that the "Real Numbers" are actually a subset of the Complex Numbers.
The Complex Numbers are also composed of two main subsets,
the "Real Numbers" and the "Imaginary Numbers".
The numbers in the set of Complex Numbers, but NOT in the set of Real Numbers are:
• the imaginary number, i, which is the square root of negative one.
• pure imaginary numbers of the form bi (where b is not zero)
• complex numbers of the form a + bi, where a and b are real numbers (and b is not zero).
Together, these values create the Imaginary Set.
Imaginary numbers are essential to the study of sciences such as electricity, quantum mechanics, vibration analysis and cartography.)
Do not confuse "imaginary" numbers with "irrational" numbers.
Not the same creatures!

|
|