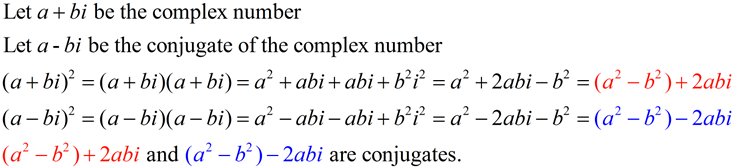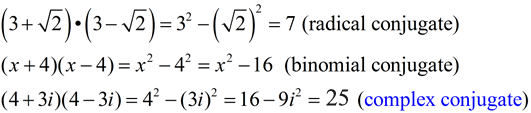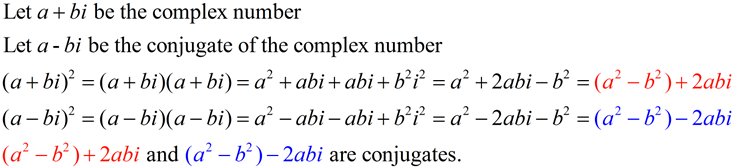Properties of Complex Numbers MathBitsNotebook.com Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Properties of Complex Numbers: (Specifically those complex numbers involving "i ".)

1. Conjugates: When we worked with radicals and with binomials in general, we discovered expressions referred to as "conjugates". A binomial expression, when multiplied by its conjugate, results in the difference of the squares of each term (with the resulting "middle terms" dropping away). This "dropping away" proved very useful when working with radicals, and became our strategy for rationalizing denominators. In a similar fashion, when a complex number is multiplied by its conjugate, the "middle terms" will drop away giving us a purely real number as the product. This is yet another strategy which will prove useful.

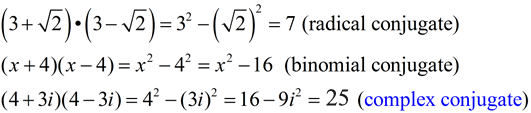
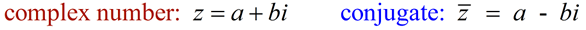
(notice the notation of "z with a bar" for the conjugate)

(a + bi) • (a - bi) = a2 + b2 (a + bi)•(a - bi) = a2 - abi + abi - b2i2 = a2 - b2i2 = a2 - b2(-1) = a2 + b2

The squares of real numbers are positive.
The sum of the squares of two real numbers creates another real number.
Therefore, a² + b² is a positive real number, and we have the following rule:

Rule: The product of a complex number and its conjugate is a positive Real Number. Example: (2 + 3i)(2 - 3i) = 4 - 6i + 6i- 9i2 = 4 - 9(-1) = 13

2. Equality: Determining if two complex numbers are equal is exactly as you would think:

a + bi = c + di when a = c and b = d

Rule: Two complex numbers are equal if and only if their real parts and their imaginary parts are respectively equal. Example: 2 + 3i = 2 + 3i

3. Closure: The complex numbers are closed under addition, subtraction. multiplication and division - when not considering division by zero. Remember that closure means that when you perform an operation on two numbers in a set, you will get another number in that set. In this case, the set is complex numbers.

Rule: If two complex numbers are added (subtracted), the sum (difference) is a complex number.

Rule: If two complex numbers are multiplied (divided - not by 0), the product (quotient) is a complex number.

4. Commutative, Associative, Distributive Properties:
All complex numbers are commutative and associative under addition and multiplication, and multiplication distributes over addition.

Commutative: For all complex numbers z1 and z2,  z1 + z2 = z2 + z1 (under addition) Ex. (3 + 2i) + (5 - 4i) = (5 - 4i) + (3 + 2i) z1• z2 = z2 • z1 (under multiplication) Ex. (3 + 2i) • (5 - 4i) = (5 - 4i) • (3 + 2i)

Associative: For all complex numbers z1, z2, z3,  z1 + (z2 + z3) = (z1 + z2) + z3 (under addition) Ex. (7 + 5i) + [(3 + 2i) + (5 - 4i)] = [(7 + 5i) + (3 + 2i)] + (5 - 4i) z1• (z2• z3) = (z1• z2) • z3 (under multiplication) Ex. (7 + 5i) • [(3 + 2i) • (5 - 4i)] = [(7 + 5i) • (3 + 2i)] • (5 - 4i)

Complex multiplication distributes over addition: For all z1, z2, z3,     z1• (z2 + z3) = z1• z2 + z1• z3 Ex. (7 + 5i) • [(3 + 2i) + (5 - 4i)] = (7 + 5i) • (3 + 2i) + (7 + 5i) • (5 - 4i)

5. Arithmetic Operations: For detailed information regarding the arithmetic of complex numbers see the following pages:

• Arithmetic of Complex Numbers (Add, Subtract, Multiply)

• Arithmetic of Complex Numbers (Divide).

6. Tidbit of Info:

Rule: The square of any complex number and the square of its conjugate are also conjugates.

How to use your TI-83+/84+ calculator with complex numbers. Click here.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Use".

Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use    Contact Person: Donna Roberts