|
Complex numbers cannot be represented on a normal set of coordinate axes.
|
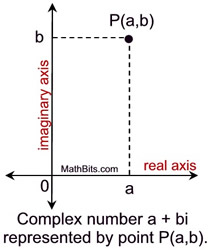
In 1806, J. R. Argand developed a method for displaying complex numbers graphically as a point in a special coordinate plane. This method, called the Argand diagram or complex plane, establishes a relationship between the x-axis (real axis) with real numbers and the y-axis (imaginary axis) with imaginary numbers.
In the Argand diagram, a complex number a + bi is represented by the point (a,b), as shown at the left. |

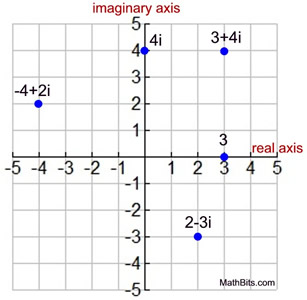
Graph the following complex numbers:
1. 3 + 4i (3,4)
2. -4 + 2i (-4,2)
3. 2 - 3i (2,-3)
4. 3 (which is really 3+ 0i) (3,0)
5. 4i (which is really 0 + 4i) (0,4)
|
 |

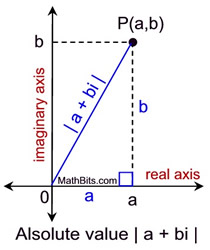
The Pythagorean Theorem will be used to determine the absolute value of a complex number.
|
|
Geometrically, the concept of "absolute value" of a real number, such as 3 or -3, is depicted as its distance from 0 on a number line. Thus, | 3 | = 3 and | -3 | = 3.

The "absolute value" of a complex number, is depicted as its distance from 0 in the complex plane.
The absolute value of a complex number
z = a + bi is written as | z | or | a + bi |.
It is a non-negative real number defined as:
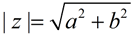 |
NOTE: Another term for " absolute value" is " modulus".
When dealing with a complex number, a + bi, the terms " absolute value", " modulus", and " magnitude" all refer to 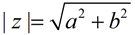 .
In the complex plane, a complex number may be represented by a single point,
or by the point and a position vector(from the origin to the point). When referenced as a vector, the term "magnitude" is commonly used to represent the distance from the origin (absolute value). |

Find | z | for :
1. z = 3 + 4i
horizontal length a = 3
vertical length b = 4
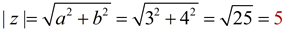
2. z = -4 + 2i
horizontal length | a | = 4
vertical length b = 2
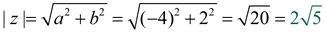 |
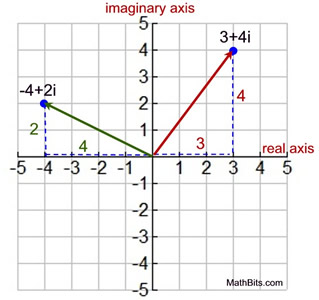 |
The complex numbers in this Argand diagram are represented as ordered pairs with their position vectors. |

Graphical addition and subtraction of complex numbers.
1. Add 3 + 3i and -4 + i graphically.
• Graph the two complex numbers as vectors.
• Create a parallelogram using these two vectors as adjacent sides. (Count off the horizontal and vertical lengths from one vector off the endpoint of the other vector.)
• The answer to the addition is the vector forming the diagonal of the parallelogram (read from the origin).
|
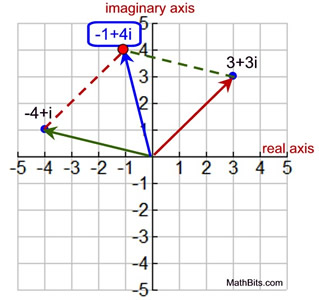 |
| • This new vector is called the resultant vector. |
2. Subtract 3 + 3i from -1 + 4i graphically.
• Subtraction is the process of adding the additive inverse.
(-1 + 4i) - (3 + 3i)
= (-1 + 4i) + (-3 - 3i)
= -4 + i
• Graph the two complex numbers as vectors.
• Graph the additive inverse of the number being subtracted. |
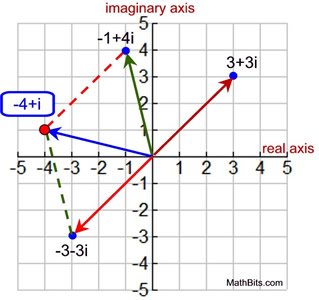 |
• Create a parallelogram using the first number and the additive inverse.
• The answer to the addition is the vector forming the diagonal of the parallelogram (read from the origin). |

|
For
calculator help with
complex vector graph
click here. |
|
|
|