smalllogo
Iteration is the process of repeating a task over and over again. When dealing with functions, iteration refers to obtaining a value from the function, using that value to obtain a subsequent value, using that subsequent value to obtain yet another value, and so on.
Example of function iteration:
f (x) = x2 + 2; starting value of x = 0.
f (0) = 2
f (2) = 6
f (6) = 38
f (38) = 1446 and so on ...
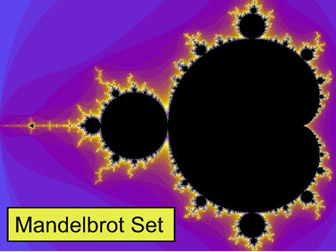bgmandelbrotpic
Example of function iteration with a complex number:
f (x) = x2 + (5 - 2i ); starting value of x = 0.
f (0) = 5 - 2i
f (5 - 2i) = (5 - 2i)2 + (5 - 2i) = 21 - 10i
f (21 - 10i) = (21 - 10i)2 + (5 - 2i) = 341 - 20i
f (341 - 20i) = (341 - 20i)2 + (5 - 2i) = 115881 - 13640i and so on ...
Notice how the values are getting larger and larger.

A function of the form f (x) = x2 + c (where c is a complex number) under iteration may produce a very special graphical display. If you plot the results of the iterations (starting with x = 0) in the complex plane, you will obtain what is called the critical orbits of c. If these critical orbits repeat (where the same point in the complex plane repeats), the complex number is in the Mandelbrot set. If the critical orbits simply move further and further away from the origin, the complex numbers are not in the Mandelbrot set.

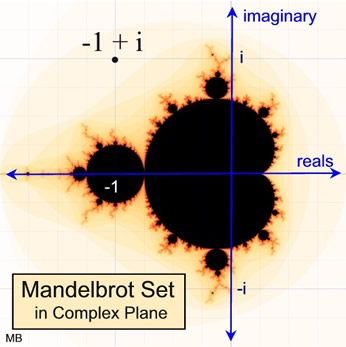
bgmandelbrot2
The black region is the Mandelbrot set. It is symmetric
with the x-axis and intersects the x-axis from -2 to ΒΌ.

The Mandelbrot set consists of all of those complex c-values for which the corresponding orbit of 0 under x2 + c does not escape to infinity.

The set is named after Benoit Mandelbrot who was one of the first mathematicians to study the set in 1980.

Infinitely Many! The decorations that adorn the main heart-shape of the set (the cardioid) are called bulbs. Each bulb in turn has infinitely many smaller decorations attached, and so on, and so on, ...
See an animated view of a Mandelbrot set.

An examination of the critical orbits of any complex number and the critical orbits of the complex conjugate will show a connection to the symmetric nature of the Mandelbrot set.
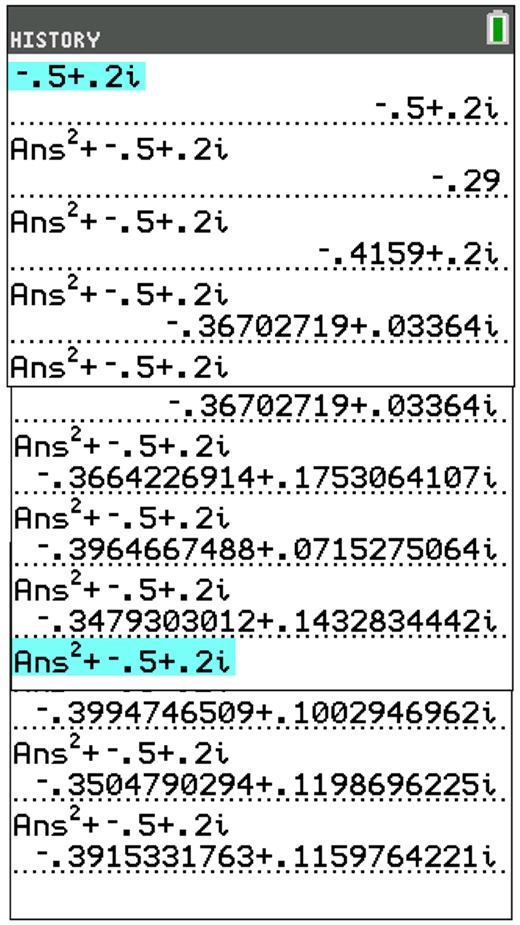
The graphing calculator can be used to help determine if the critical orbits repeat and lie in the Mandelbrot set.
Place the calculator in a + bi mode.

f (x) = x2 + (-0.5 + 0.2i )
The calculator screens below show that the iterations of this function are demonstrating a repeating nature of the orbits. This tells us that the orbits will fall in the Mandelbrot set.
If the iterations had started to grow larger and larger (escaping to infinity), the orbits would fall outside of the Mandelbrot set. brotlist
mandelbrot3
mandelbrot4

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".

Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use    Contact Person: Donna Roberts