|
In this lesson, we will begin our work with the number e.
e is an irrational number, approximately 2.71828183,
named after the 18th century Swiss mathematician, Leonhard Euler. |
The number e is one of the famous numbers in mathematics. As your mathematical studies progress from Algebra 2 through Calculus, you will discover that the role of e in mathematics is equal in importance to
that of the number π.
π is the ratio between circumference and diameter shared by all circles.
e is the base rate of growth shared by all continually growing processes.
|
 |
There are 5 numbers that are considered the "five most important numbers in mathematics". The five numbers are 0, 1, π, e, and i. Now, you know them all! |

Natural Exponential Function |
|
|
When the base, b, of the exponential function y = bx, is replaced with e,
we have the natural exponential function.
The natural exponential function may be expressed as y = ex or as y = exp(x).
In functional notation: f (x) = ex or f (x) = exp(x)
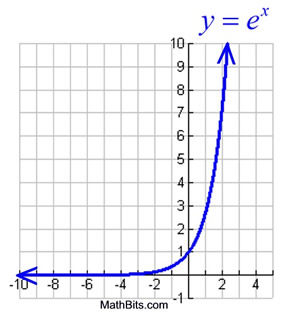
The graph of the function defined by f (x) = ex
looks similar to the graph of f (x) = bx where b > 1.
This natural exponential function is simply a "version" of the exponential function f (x) = bx
As such, the characteristics of this graph are similar to the characteristics of the exponential graph.
Domain: All Reals
Range: y > 0
|
|

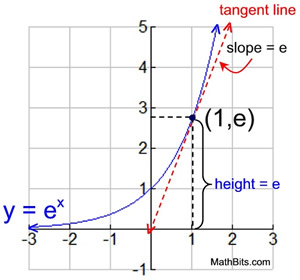
The function f (x) = ex is the only function, of this form, where the slope of a tangent to the curve at any point is equal to the height of the curve at that point.
This fact will look
"more exciting"
when you get to Calculus. |
|
|
 |
|

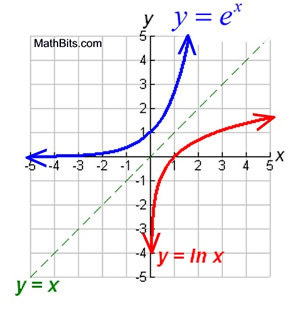
Since f (x) = ex is a one-to-one function, we
know that its inverse will also be a function.
But what is the equation of the inverse of f (x) = ex ?
The equation of the inverse is:
y = loge x = ln x
and is called the natural logarithmic function.
This new function is simply a
"version" of
y = logb x where b > 1.
|
|
On the Graph: Notice how (0,1) from f(x) = ex becomes (1,0) for y = ln(x).
The coordinates switch places between a graph and its inverse. |
|

Natural Logarithmic Function |
|
|
When the base, b, of the logarithmic function, y = logb x, is replaced with e,
we have the natural logarithmic function.
The natural logarithmic function, y = loge x, is more commonly written y = ln x.
In functional notation: f (x) = ln x
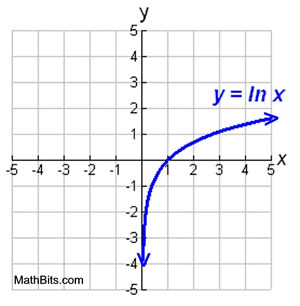
The graph of the function defined by y = ln x,
looks similar to the graph of y = logb x where b > 1.
The characteristics of this new function are similar to logarithmic function characteristics we already know.
Domain: x > 0
Range: All Reals
|
|

|
For help with exponential expressions on your calculator, click here.
|
|
|
|
For help with logarithms on
your calculator,
click here.
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|