|
An exponential inequality is one in which a variable occurs in the exponent.
|
|
As was done with solving exponential equations, we will examine
two algebraic methods
for solving exponential inequalities:
Method 1: Using a Common Base and Method 2: Using Logarithms
A graphical solution will be offered as a check on the algebraic solutions.
Things to keep in mind when working with exponential inequalities:
• an exponential function bxis always positive. (bx < 0 has no solution)
• an exponential function is increasing when b > 1.
• an exponential function is decreasing when 0 < b < 1.
• as was done in linear inequalities, multiplying (or dividing) by a negative value reverses the inequality sign. |
|
Examples on this page will display answers rounded to nearest thousandth when needed.

Method 1: Common (same) Base
If the bases are the same (or can be rewritten to be the same),
set up an inequality using the exponents. |
|
For exponential inequalities with the same base:
(1) For b > 1, bx > by if and only if x > y.
(2) For 0 < b < 1, bx > by if and only if x < y. |
* Inequality Direction:
If b > 1, direction unchanged
If 0 < b < 1, direction flips |
|
Let's take a look a couple of examples, and the graphs to illustrate the answers.
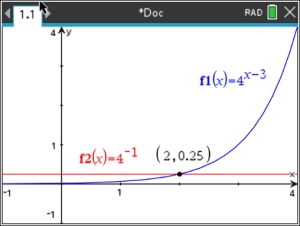
 4x-3 > 4-1
• The base 4 is greater than 0, so "keep the direction" of the
inequality. 4x-3 > 4-1
• The base 4 is greater than 0, so "keep the direction" of the
inequality.
• Set up the exponents with a "greater than" symbol:
x - 3 > -1
• Solve for x:
x > 2 In interval notation: (2,∞) |
 |
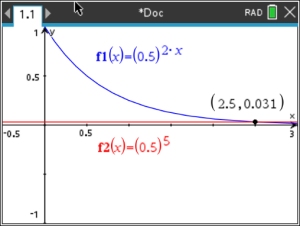
 (0.5)2x > (0.5)5 (0.5)2x > (0.5)5
• The base 0.5 is in the interval 0 < x < 1, so "reverse the direction" of the inequality.
• Set up the exponents with a "less than" symbol (flip):
2x < 5
• Solve for x: x < 5/2 In interval notation: (-∞, 5/2) |
 |

Method 2: Bases Not the Same
If the bases are not the same,
take the logarithm of both sides. |
|
For exponential inequalities with different bases, take the logarithm of both sides. Choose the logarithm "base" such that an inverse relationship can be applied to simplify the inequality.
There is no flipping of the inequality in these solutions.

A logarithmic inequality is simply an inequality containing one
(or more) logarithms with variable expressions. |
|
Things to keep in mind when working with logarithmic inequalities:
• a logarithm's domain is positive
• use exponentiation determined by the log's base.
• if the base is greater than 1, the inequality direction (sign) remains the same.
• if the base is between 0 and 1, the inequality direction (sign) flips.
|
|
Examples on this page will display answers rounded to nearest thousandth when needed.
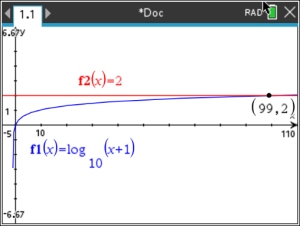
 log(x+1) < 2
• log (with no base indicated) is base 10. log(x+1) < 2
• log (with no base indicated) is base 10.• The domain must be positive: x + 1 > 0, so x > -1.
• use exponentiation: 10log(x+1) < 102
and get x + 1 < 102, and x < 99.
• Solution: -1 < x < 99 In interval notation: (-1,99) |
 |
 ln(2x - 1) > ln(x + 3)
• The base is e. ln(2x - 1) > ln(x + 3)
• The base is e.
• The domain is 2x - 1 > 0 AND x + 3 > 0
So x > 1/2 AND x > -3. Both are true when x > 1/2.
• Solve for x: eln(2x-1) > e ln(x+3)
(2x - 1) > (x + 3) gives 2x - 1 > x + 3, x > 4
• Solution: x > 1/2 and x > 4, giving x > 4In interval notation: [4, ∞) |
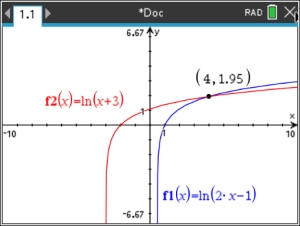 The y-values of f1 become larger than the The y-values of f1 become larger than the
y-values of f2 at x = 4 and beyond. |
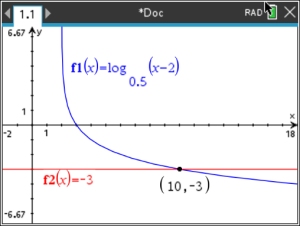
 log0.5(x - 2) > -3
• The base is 0.5. This base is between 0 and 1, so the inequality will flip. log0.5(x - 2) > -3
• The base is 0.5. This base is between 0 and 1, so the inequality will flip.
• The domain is x - 2 > 0 , so x > 2.
• Solve for x: 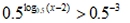 Flip: x - 2 < 0.5-3 gives x - 2 < 8, x < 10
• Solution: x > 2 and x < 10 giving 2 < x < 10
In interval notation: (2,10) |
 |

|
For help with inequalities
the on
calculator,
Click here. |
|
|
|
For help with inequalities
on
the
calculator,
Click here.
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|