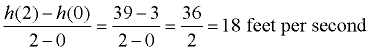|
 Linear Functions: Linear Functions: |
You are already familiar with the concept of "average rate of change".
When working with straight lines (linear functions) you saw the "average rate of change" to be:
The word "slope" may also be referred to as "gradient", "incline" or "pitch", and be expressed as:

A special circumstance exists when working with straight lines (linear functions), in that the "average rate of change" (the slope) is constant. No matter where you check the slope on a straight line, you will get the same answer.
|
|
 Non-linear Functions: Non-linear Functions: |
When working with non-linear functions, the "average rate of change" is not constant.
The process of computing the "average rate of change", however, remains the same as was used with straight lines: two points are chosen, and 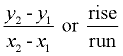 is computed. is computed.
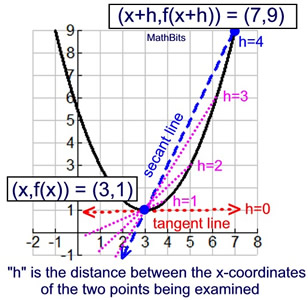
FYI: You will learn in later courses that the "average rate of change" in non-linear functions is actually the slope of the secant line passing through the two chosen points. A secant line cuts a graph in two points. |
|
When you find the "average rate of change" you are finding the rate at which (how fast) the function's y-values (output) are changing as compared to the function's x-values (input).
When working with functions (of all types), the "average rate of change" is expressed using function notation.
Average Rate of Change
For the function y = f (x) between x = a and x = b, the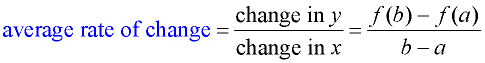 ( b - a ≠ 0)
|
 A closer look at this "general" average rate of change formula: A closer look at this "general" average rate of change formula: |
While this new formula may look strange, it is really just a re-write of 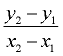 . .
Remember that y = f (x).
So, when working with points (x1, y1) and (x2, y2), we can also write them as
the points 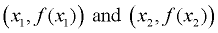 . .
Then our slope formula can be expressed as 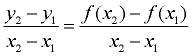 . .
If we rename x1 to be a, and x2 to be b, we will have the new formula.
The points are 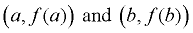 , and the , and the
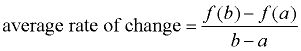 where ( b - a ≠ 0) where ( b - a ≠ 0). |
|
If instead of using (a, f (a)) and (b, f (b)) as the points, we use the points
(x, f (x)) and (x + h, f (x + h)), we get:
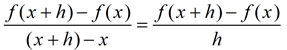
This expression was seen in evaluating functions. It is a popular expression, called the difference quotient, and will appear in future courses. Notice, as h approaches 0 (gets closer to 0), the secant line becomes a tangent line. |
 |
|
Average Rate of Change
The average rate of change is the slope of the secant line
between x = a and x = b on the graph of f (x).
The secant line passes through the points (a, f (a)) and (b, f (b)).
|
 Negative Rate of Change: Negative Rate of Change: |
The graph at the right shows an average rate of change on the function f (x) = x2 - 3 from point (-2,1) to (0,-3). The segment connecting the points is part of a secant line.
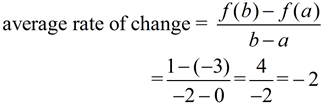
This average rate of change is negative.
|
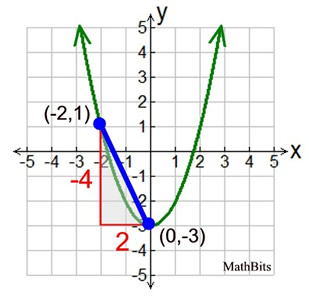 |
 An average rate of change of 4/(-2), means that for every 2 units of movement to the right on the x-axis on this interval, there will be 4 units of change on the y-axis. The negative sign indicates that the y-change movement will be in a negative direction (downward) producing at least a decreasing portion of the graph somewhere on this interval (if not the entire interval). An average rate of change of 4/(-2), means that for every 2 units of movement to the right on the x-axis on this interval, there will be 4 units of change on the y-axis. The negative sign indicates that the y-change movement will be in a negative direction (downward) producing at least a decreasing portion of the graph somewhere on this interval (if not the entire interval).
An accepted interpretation: an average rate of change of -2, for example, is to be interpreted as a "rate of change of 2 in a negative direction". [NOTE: The "amount" of a rate of change is determined by its absolute value. A rate of change of -3 would be considered "greater" than a rate of change of +2, assuming the units are the same in both cases.]
Average Rate of Change and Increasing/Decreasing
When the average rate of change is positive, the graph has increased on that interval.
When the average rate of change is negative, the graph has decreased on that interval.
|
Did you notice the "careful" wording relating to " has increased" and " has decreased" in the box above?
The "increased " statement, for example, does NOT say that the function will be necessarily increasing on the ENTIRE interval. It may simply be increasing on a portion of the interval.
We can say that: "If a function is continually increasing on an interval, its average rate of change on that interval is positive."
But we cannot say that: "If a function's average rate of change on an interval is positive, the function is continually increasing on that interval." |
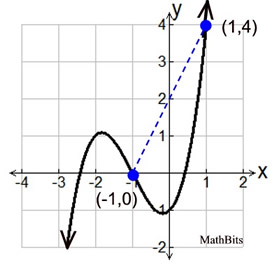 |
See the counterexample at the right for function f (x) = x3 + 3x2 + x - 1.
From (-1,0) to (1,4) the average rate of change is (4-0)/(1-(-1)) = +2, a positive value. But the graph is NOT INCREASING on the entire interval from (-1,0) to (1,4). Yes, MORE of the interval is increasing than is decreasing, but the entire interval is not increasing. |
 Zero Rate of Change: Zero Rate of Change: |
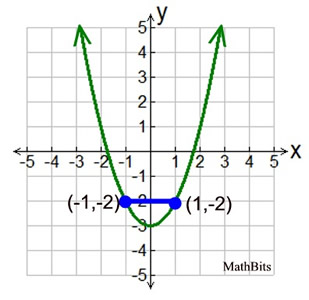
The graph at the right shows average rate of change on the function f (x) = x2 - 3 from point (-1,-2) to (1,-2).
This average rate of change is zero.
A zero rate of change is achieved when f (b) = f (a) giving a numerator of zero.
|
 |
When the average rate of change is zero, the sum of all possible positive slopes and negative slopes on the interval will be zero.
The sum of the possible positive slopes cancels out the sum of the possible negative slopes.

 Examples: Examples: |
 Finding average rate of change from a table. Finding average rate of change from a table.
Function f (x) is shown in the table at the right.
Find the average rate of change over the interval 1 < x < 3.
Solution:
If the interval is 1 < x < 3, then you are examining the points (1,4) and (3,16). From the first point, let a = 1, and f ( a) = 4. From the second point, let b = 3 and f ( b) = 16.
Substitute into the formula:
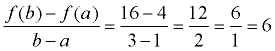
|
|
The average rate of change is 6 over 1, or just 6.
The y-values change 6 units every time the x-values change 1 unit, on this interval. |

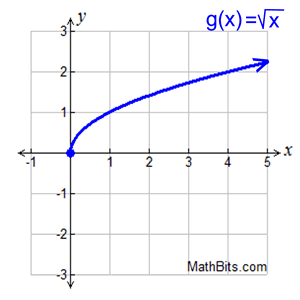
 Finding average rate of change from a graph. Finding average rate of change from a graph.
Function g (x) is shown in the graph at the right.
Find the average rate of change over the interval
1 < x < 4.
Solution:
If the interval is 1 < x < 4, then you are examining the points (1,1) and (4,2), as seen on the graph. From the first point, let a = 1, and g ( a) = 1. From the second point, let b = 4 and g ( b) = 2.
Substitute into the formula: 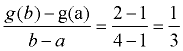
|
|
The average rate of change is 1 over 3, or just 1/3.
The y-values change 1 unit every time the x-values change 3 units, on this interval. |

 Finding average rate of change from a word problem. Finding average rate of change from a word problem.
A ball thrown in the air has a height of h(t) = - 16t² + 50t + 3 feet
after t seconds.
a) What are the units of measurement for the average rate of change
of h?
b) Find the average rate of change of h between t = 0 and t = 2?
|
|
Solution:
a) In the formula, 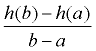 , the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball. , the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball.
b) Start by finding h(t) when t = 0 and t = 2, by plugging the t values into h(t).
h(2) = -16(2)² + 50(2) + 3 = 39
h(0) = -16(0)² + 50(0) + 3 = 3
Now, use the average rate of change formula:
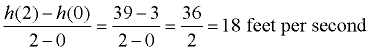

|
 Comparing Comparing average rates of change .
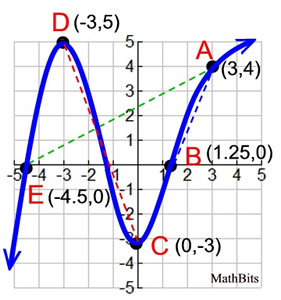
Given the function shown at the right.
State whether the following statements are TRUE or FALSE:
a) average rate of change from B to A is greater than average rate of change from E to A.
b) average rate of change from B to A is greater than average rate of change from D to C.
Solution:
a) average rate of change on B to A =
(4 - 0)/(3 - 1.25) ≈ 2.285
average rate of change on E to A =
(0 - 4)/(-4.5 - 3) ≈ 0.533
TRUE
|
|
b) average rate of change on B to A ≈ 2.285
average rate of change on D to C = (5 - (-3))/(-3 - 0) ≈ -2.667
READ CAREFULLY!!!
FALSE
We know mathematically that 2.285 > -2.667. In this situation, however, the negative sign simply designates "direction" (decreasing in this case). The decrease from D to C is changing at a rate faster than the rate of increase from B to A. The rate of change of 2.667 is greater than that of 2.285. So, the answer to the question is FALSE.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

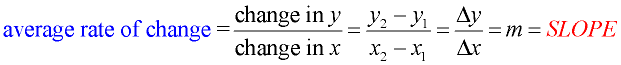

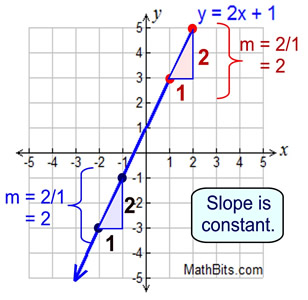
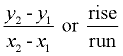 is computed.
is computed.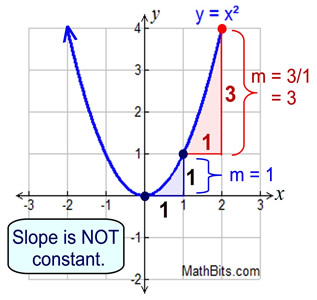
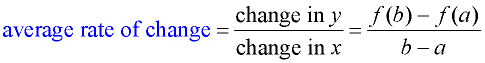 ( b - a ≠ 0)
( b - a ≠ 0)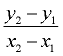 .
.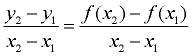 .
.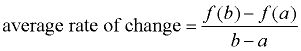
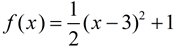

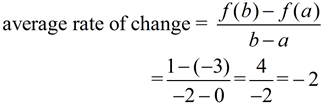


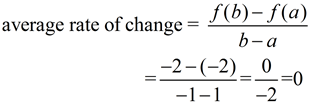

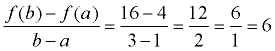
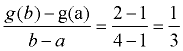

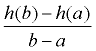 , the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball.
, the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball.