|
Directions: Read carefully. Choose the best answers.
1. |
Write the equation for the graph of function
g(x), obtained by shifting the graph of
f (x) = x² three units left, stretching the graph vertically by a factor of two, reflecting that result over the x-axis, and then translating the graph up four units.
|
 |
|
|
|
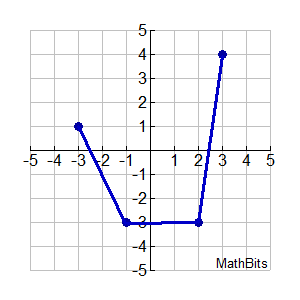
2. |
The graph of f ( x) is shown at the right on the domain [-3,3].
A function k ( x) is defined as
k ( x) = f ( x + 1) - 2.
Sketch the graph of k (x).
|
 |
|
|
|
3. |
Describe the transformations that would produce the graph of the second function from the graph of the first function, for sections a, b and c.
|
|
|
|
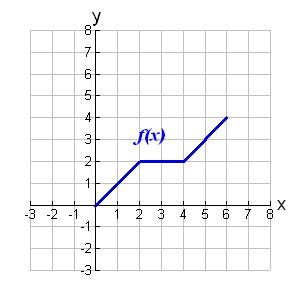
4. |
Given the graph of the function
f (x) shown at the right on the interval [0,6].
Sketch the graphs of:
| a. f (x + 1)
b. f (x) - 2
c. f (-x)
d. -f (x)
e. 2 f (x) |
|
|
| |
|
5. |
Let x represent the length of a side of a square and an edge of a cube.
a. Graph the area of the square as a function of x.
b. On the same axes, graph the surface area of the cube as a function of x.
c. Describe the relationship between these two graphs using transformational terms.
|
|
|
|
6. |
Transform the function f (x) = ex with a vertical stretch by a factor of 3, followed by a translation 5 units to the right.
a. Write an equation for the transformed function.
b. Graph the transformed function.
|
|
|
|
7. |
Write the equation for the graph shown at the right. The line segments shown are straight and intersect at the point (4,-2). The x-intercepts are (-2,0) and (6,0).
Assume that the parent function was
y = | x |.
|
|
|
|
8. |
Given: f (x) = x2 - 2x
a. Determine an expression for h(x), if h(x) = f (-x).
b. Determine an expression for g(x), if g(x) is represented by the rotation of 180º of f (x) about the origin.
c. Rotate f (x) 90º about the origin. Find the coordinates of the point(s)
for which x = -1, under the rotation.
|
|
|
9. |
Consider the relationship between Fahrenheit and Celsius temperatures. Using your graphing calculator, graph these two functions on the same set of axes:
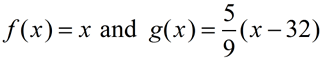
a. Describe in transformational terms, how the first graph becomes the second graph.
b. At what temperature are the Fahrenheit and Celsius readings the same? |
|
|
10. |
A function is defined as f (x) = x3 - 4.
Sketch the graph of f (x) and f -1 (x) on the same axis and describe in transformational terms the relationship between these two graphs.
|
|
|
11. |
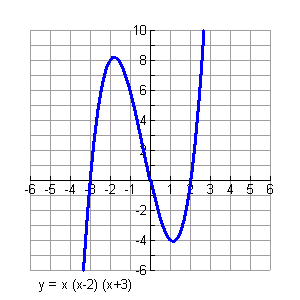
Given: the function shown at the right y = x( x - 2)( x + 3)
a. Graph the given function with a vertical stretch of factor ½ and a translation of 3 units to the left.
b. Graph the given function with a translation of 6 units to the right.
c. Describe the transformation that occurred to the given function, if a new function's equation is
y = 4 x( x - 2)( x + 3).
d. Describe the transformation that occurred to the given function, if a new function's equation is 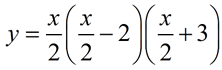 |
|
|
12. |
Given: function, y = x2 - 1 graphed in blue.
Match the transformation equations shown below with their corresponding graphs.
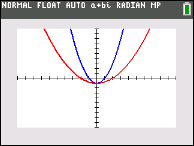 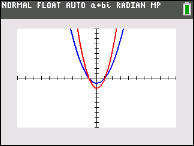 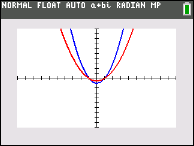
Possible equation matches (not in matching order):
(1) y = 2 (x2 - 1)
(2) y = ½ (x2 - 1)
(3) y = (½ • x)2 - 1
|
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|