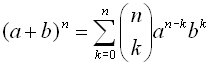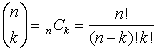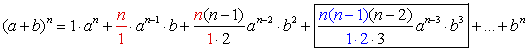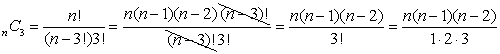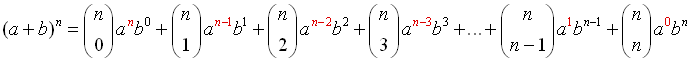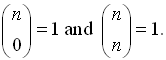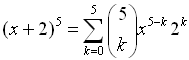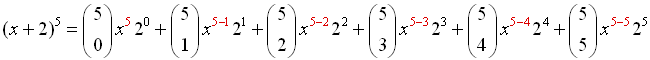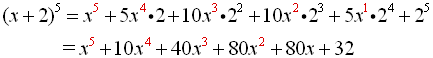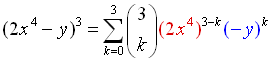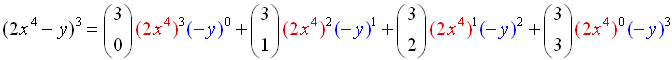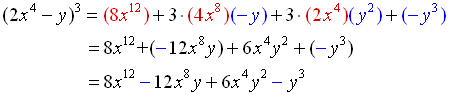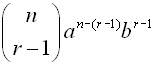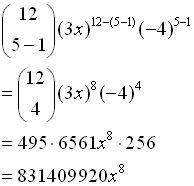|
You are asked to expand (x + 7)10.
You will need to multiply (x + 7) times itself 10 times.
(x + 7)
(x + 7)
(x + 7)
(x + 7)
(x + 7)
(x + 7)(x + 7)
(x + 7)
(x + 7)
(x + 7)
This could take forever - well, at least quite a while!
Is there an easier way to arrive at this expansion?
Let's investigate!
 |
When the binomial expression (
a + b)
n is expanded, there are certain patterns that are noticeable.
Take a look at the expansions when the values of
n range from 0 to 4.
 |
If you "pull off" the coefficients of the terms (shown in red), you will discover that the coefficients form a triangle known as
Pascal's Triangle. |
Pascal's Triangle can be generated by following a certain pattern.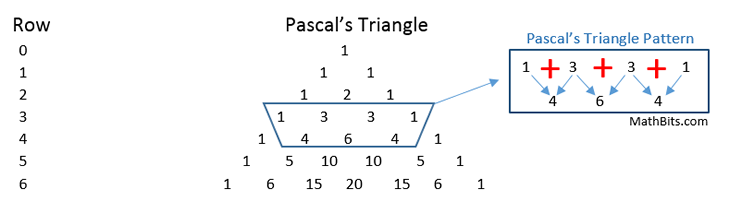
Pascal's Triangle Pattern: The two outside edges of the triangle are comprised of ones.
The other terms are each the sum of the two terms immediately above them in the triangle.
Notice the symmetry of the triangle.
The triangle can grow for as many rows as you desire,
but the work becomes more tedious as the rows increase.

In addition to the observation that the coefficients of a binomial expansion
are the entries that create Pascal's triangle, there are several other interesting patterns
and observations regarding the expansion of (a + b)n.
1. |
The expansion is a series (an adding of the terms, a summation). |
2. |
The number of terms in each expansion is one more than n. (terms = n + 1) |
3. |
The power of a starts with an and decreases by one in each successive term ending with a0.
The power of b starts with b0 and increases by one in each successive term ending with bn. |
4. |
The power of b is always one less than the "number" of the term.
The power of a is always n minus the power of b.
|
5. |
The sum of the exponents in each term adds up to n. |
6. |
The coefficients of the first and last terms are each one. |
7. |
The coefficients of the middle terms form an interesting (but not easily recognizable) pattern where each coefficient can be determined from the previous term. The coefficient is the product of the previous term's coefficient and a's index (power), divided by the "number" of that previous term.
Check it out: 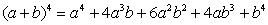
The second term's coefficient is determined by a4: 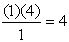 |
To Get Coefficient
From the Previous Term:
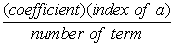 |
|
The third term's coefficient is determined by 4 a3b: 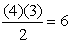 |
This pattern will eventually be expressed as a combination of the form n C k. |
When these patterns and observations are pulled together, along with some mathematical
syntax,
a theorem is formed pertaining to the expansion of binomial terms:
Binomial Theorem
(or Binomial Expansion Theorem)
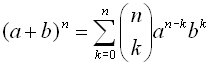
|
|
Most of the syntax used in this theorem should look familiar. The 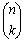 notation is another way of writing a combination such as n C k (read " n choose k").
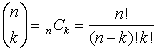 |
|
|
Expand: (x + 2)5 |
Let a = x, b = 2, n = 5 and substitute into the Binomial Theorem.
Do not substitute a value for k. |
|
|
This is a good time to put your graphing calculator to work to calculate the combinations.
See calculator link at the bottom of this page.
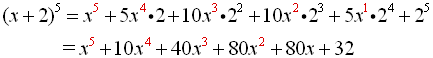 |

|
Expand: (2x4 - y)3 |

The "a" value in this problem is the expression "2x4".
Also, the sign is negative making the "b" value "-y".
((2x4) + (-y))3
Let a = (2x4), b = (-y), n = 3 and substitute. |
|
|
Be sure to raise the entire parentheses to the indicated power. Watch out for signs.
Use your calculator for the combinations (see calculator link at bottom of page).
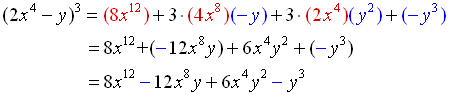 |

Finding a Particular Term in a Binomial Expansion |
What if you are asked to find just "one" term in a binomial expansion,
such as just the 5th term of (3x - 4)12 ?
Let's call the term we are looking for the rth term. From our observations, we know that the coefficient of this term will be n C r-1, the power of b will be r - 1 and the power of a will be n minus the power of b. Putting this information together gives us a formula for finding the rth term of a binomial expansion.
The rth term of the expansion of ( a + b) n is: 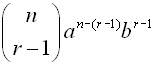
|
|
Find 5th term of (3x - 4)12 |
Let r = 5, a = (3 x), b = (-4), n = 12 and substitute.
Use your calculator for the combination.
Be sure to use the parentheses!!
Be careful to raise the entire parentheses to the indicated power.
|
|
 |
Check out how to use your graphing calculator with the binomial theorem. Click here. |
|
|
|
Check out how to use your graphing calculator with the binomial theorem. Click here. |
|
|