|
 Dividing a Polynomial by a Monomial:
|
When dividing a polynomial by a monomial,
divide EACH term of the polynomial by the monomial.
Remember to use the quotient rule for exponents. 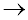
|
|

When dividing a polynomial by a monomial, the number of terms in the polynomial equals the number of terms in the answer. |
|
|
When dividing by a monomial, numbers (or expressions)
do not "cancel" and disappear!
A number (or expression) divided by itself equals one. |
|
Another way of looking at "dividing by a monomial" is multiplying by the reciprocal of the monomial. See Example 2.
|
|
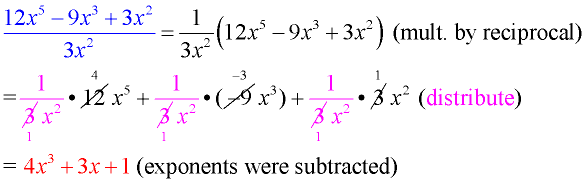 |

 Dividing a Polynomial by a Binomial: (factorable situations only) Dividing a Polynomial by a Binomial: (factorable situations only)
|
When dividing a polynomial by a binomial, FACTOR completely both the numerator and denominator (the dividend and divisor) before reducing. Reduce the greatest common factors from the numerator and denominator. |
|
The terms in a binomial cannot be separated from one another when reducing. For example, in the binomial 4x - 1, the 4x cannot be reduced by itself. You must reduce the entire expression 4x - 1. |
|
|
Factor the numerator.
Reduce the common factor of x + 3.
|
|
|
Factor the numerator.
Reduce the common factor of a - 5.
|
|
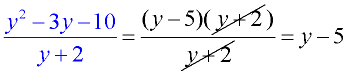
|
Factor the numerator.
Reduce the common factor
y + 2.
|
|
|
Factor the numerator.
Factor the denominator.
Reduce the common factor of x + 2.
|
 Sneaky one!!
Sneaky one!!
|
|
7 - x and x - 7 are "almost" the same, except that the signs of the terms are opposite one another. To create a situation that will allow for reducing, factor out -1 from one of these binomials. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

