|
Directions: Solve the following questions pertaining to polynomial graphs, zeros, and end behavior.
Please NO GRAPHING CALCULATORS for this practice page.
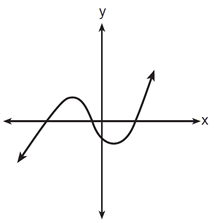
1. |
Which of the following characteristics does not pertain to the graph shown at the right?
|
|
|
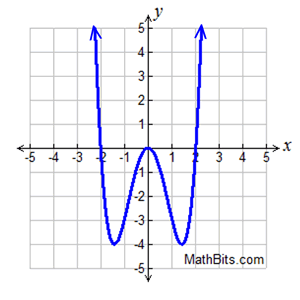
2. |
Which of the following characteristics does not pertain to the graph shown at the right?
Assume all roots are real.
|
|
|
3. |
Find the zeros (and each multiplicity) for the polynomial P(x) = x2(x - 3)2(x + 1)(x + 4)3 .
The number in parentheses is the multiplicity of the preceding root (zero).
|
|
|
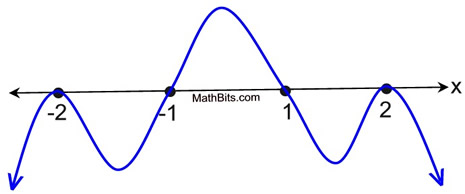
4. |
a) Assuming only real roots, what is the degree of the polynomial function sketched below?
|
|
5. |
• State the roots of the polynomial
P( x) = x ( x + 2) 2 ( x - 3) 3.
• Indicate whether the graph crosses the
x-axis at each root, or just touches the x-axis.
• Draw a sketch of the graph.
|
|
|
6. |
Which of the equations at the right, when graphed, will intersect with the x-axis only once? Explain how you arrived at your answer.
|
A: y = 2x3 - 16x2 + 32x
B: y = x3 - 2x2 + 4x - 8
C: y = x3 - 3x2 - x + 3 |
|
|
7. |
Given the conditions stated at the right, determine:
a) the degree of the polynomial function
b) the end behavior
c) a rough sketch
Explain your answers.
|
Conditions:
• the leading coefficient is positive
• Root x = -3 multiplicity 2
• Root x = 2 multiplicity 1
• Root x = -1 multiplicity 1 |
Assume only real roots. |
|
8. |
The polynomial function P( x) = x3 - 25 x.
a) Factor and determine the roots.
b) Determine the end behavior of the graph.
c) Make a sketch of the graph.
Explain how you arrive at your answers.
|
|
|
9. |
Given the polynomial function
f (x) = (2x + 1)(x - 3)(x + 1)
a) What is the y-intercept of the graph of the function?
b) Describe the end-behavior of this function.
c) For what values of x is f (x) > 0?
d) How many relative maximums does this function have?
|
|
|
10. |
P(x) =
2x3 + 4x2 - 14x + 8
has (x + 4) as a factor.
a) Factor the polynomial into three linear terms.
b) Describe the end behavior.
c) Identify all intercepts.
d) Describe how you would go about sketching the graph of a function defined by this polynomial, without using a graphing calculator.
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|