When dealing with polynomial functions, it is possible to determine the end behavior of the graph prior to drawing the graph. This skill is based upon the relationship between a power function and the polynomial function being examined

Power functions are the building blocks for the end behavior of polynomial functions.

The "end behavior" of a polynomial function describes how the graph behaves as the x-variable (input) approaches positive infinity (x → +∞) and approaches negative infinity (x → -∞). (i.e., the "ends" of the graph)

In the previous lesson on Power Functions, we discovered that if you know:
• whether the degree of a power function is odd or even, and
• whether the coefficient is positive or negative,
you can identify the end behavior of that power function without graphing.

Power Function f(x) = kxp	Coefficient k > 0	Coefficient k < 0
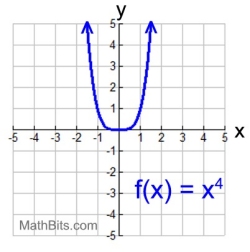
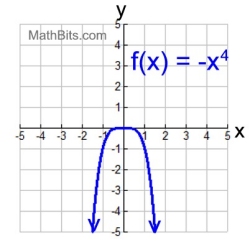
The degree (p) is EVEN End behavior: k > 0, both up k < 0, both down	x → +∞,   f (x) → +∞ x → -∞,   f (x) → +∞	x → +∞,   f (x) → -∞ x → -∞,   f (x) → -∞
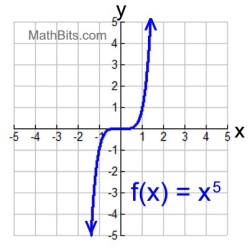
The degree (p) is ODD End behavior: k > 0, left down, right up k < 0, left up, right down	x → +∞,   f (x) → +∞ x → -∞,   f (x) → -∞	x → +∞,   f (x) → -∞ x → -∞,   f (x) → +∞

When dealing with polynomials, the highest degree in the polynomial will dominate the function's behavior as x approaches positive or negative infinity.

When | x | gets very large, the leading term (a_nxⁿ) in the polynomial function grows much faster than all of the other terms combined. Thus, the behavior of the function at its "ends" (approaching positive or negative infinity) will resemble the behavior of just the leading term, which by itself, is a power function, f (x) = a_nxⁿ.

The end behavior of a polynomial function will be the same as the end behavior of the leading term power function.

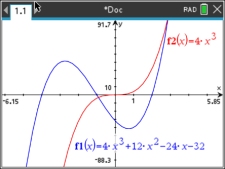
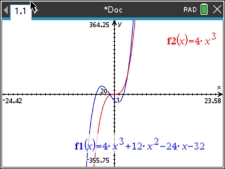
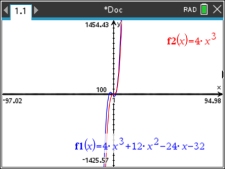
For example, the polynomial function, f (x) = 4x³ +12x² - 24x - 32
will have the same end behavior as the power function f (x) = 4x³.

In this case, the end behavior for both graphs will be
x → +∞,   f (x) → +∞
x → -∞,   f (x) → -∞

The end behavior of a polynomial function can be determined by
looking at only the highest powered term (as a power function).

Let's take a look at what happens when we graphically compare
(polynomial function) f (x) = 4x³ + 12x² - 24x - 32 and (power function) f (x) = 4x³
by "zooming out" the window.

Each "zoom out" will get us closer to seeing the ends of the graphs from a wider perspective.

Window: x:   [-6.15 to 5.85] y:   [-88.3 to 91.7]

Window: x:   [-24.42 to 23.58] y:   [-355.75 to 364.25]

Window: x:   [--97.83 to 94.98] y:   [-1425.57 to 1434.43]

Focus on what is happening at the ends of the graphs.
As we stand back and look at these functions, we can see wider views
that show us more of the "ends" of the graphs.
These views show that the "ends" are coming closer together -- to the point
where they can eventually be viewed as being the same.

Thus, the "ends" of the polynomial function and the "ends" of the power function will coincide.