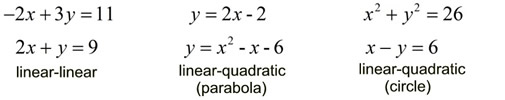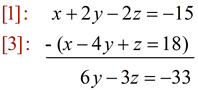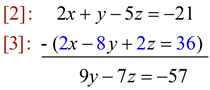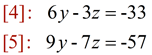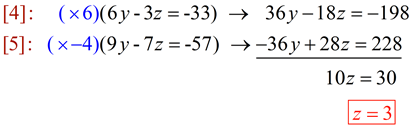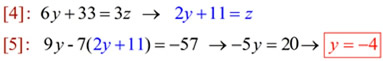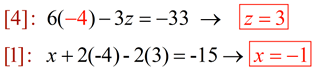Up to this point, we have been working with 2x2 systems of two equations involving two variables, such as x and y. We have solved linear-linear systems consisting of two straight lines, and linear-quadratic systems consisting of one straight line and either one parabola or one circle.

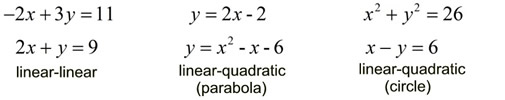
We found, when solving these 2x2 systems, that there are three basic methods of arriving at the solution: an algebraic solution by elimination, an algebraic solution by substitution, and a graphical solution.

We will be examining how well these three methods of solution can be used to tackle 3x3 systems of three equations involving three variables. All of the variables will be of degree 1. x + 2y - 2z = -15 2x + y - 5z = -21 x - 4y + z = 18 Algebraic Solution by Elimination

Steps to Solving by Elimination: This process will be similar to that used for 2x2 systems, only repeated more times.	[1]:     x + 2y - 2z = -15 [2]:    2x + y - 5z = -21 [3]:      x - 4y + z = 18	This method works well!
1. Start with any two equations to eliminate a variable. Choose the easiest variable to eliminate. Then choose a different pair of equations and eliminate the same variable. You will be left with a 2x2 system. To eliminate "x", subtract [3] from [1] and get: 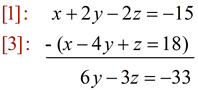           To eliminate "x" again, multiply [3] by 2, subtract from [2] and get:
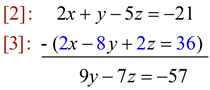2. Now, solve the new 2x2 system by elimination. Set up the new 2x2 system: 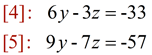To eliminate "y", multiply [4] by 6, [5] by -4, and add: 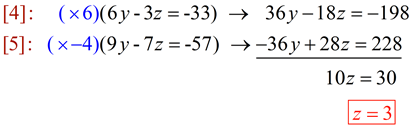Now that we have z = 3, substitute z back into [4] or [5] to find the value of y:
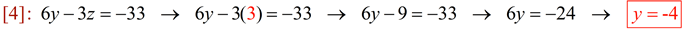3. Substitute the solutions for z and y back into [1], [2] or [3] to find the value of x: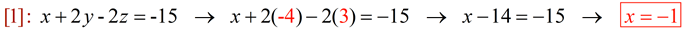
4. ANSWER:      x = -1; y = -4; z = 3      or      {-1, -4, 3}

This method shows "one" way to arrive at the answers. Other equations could have been chosen throughout the process.

Algebraic Solution by Substitution

Steps to Solving by Substitution: This process will be similar to that used for 2x2 systems, but will require more simplification.	[1]:     x + 2y - 2z = -15 [2]:    2x + y - 5z = -21 [3]:      x - 4y + z = 18	This method works well!
1. Start with any of the equations. Pick any variable in the equation and solve for it. We will pick equation [3], and solve for x.    [3]:     x - 4y + z = 18               x = 18 + 4y - z
2. Now, substitute this value for x into the other two equations, [1] and [2], and simplify. Substitute into [1]: [1]:    x + 2y - 2z = -15           (18 + 4y - z) + 2y - 2z = -15            6y - 3z = -33 Substitute into [2]: [2]:   2x + y - 5z = -21          2 (18 + 4y - z) + y - 5z = -21          9y - 7z = -57
3. You now have a system with two equations and two unknowns, y and z. You could solve these two equations by any method, but we will continue with the substitution method. Set up the new 2x2 system: 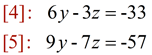Solve [4] for z, then plug into [5] for z, and solve: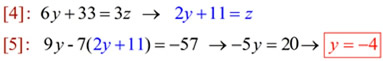
4. Substitute y = -4 into [4] and solve for z. Then plug both values into [1], [2] or [3] and solve for x.
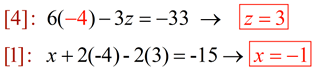5. ANSWER:      x = -1; y = -4; z = 3      or      {-1, -4, 3}

This method shows "one" way to arrive at the answers. Other equations could have been chosen throughout the process.

Graphical Solution

This method is problematic for 3x3 systems.

When working with a 2x2 system, for example, where the two variables are each of degree one (such as x and y), we are dealing with two straight lines. We can solve such a system by graphing the lines on a set of axes in the 2-dimensional Cartesian plane and finding the point of intersection. Such graphing may be done by hand or on a graphing calculator. There is also the possibility that we may be dealing with "strange" situations such as the lines being parallel (no solution), or the lines coinciding (lying on top of one another with an infinite number of solutions).

When working with a 3x3 system where the three variables are each of degree one (such as x, y, and z), we are dealing with the 3-dimensional Cartesian space. This poses a problem in that graphing in 3-D can be difficult to visualize since we are looking for the intersection of three planes (not three lines). Most graphing calculators do not graph in 3-D. And like the "strange" situations we encountered in 2-D, there will also be the possibility of "strange" situations occurring in 3-D space.

Let's take a quick look at how graphing is accomplished in 3-D:
The 3-D coordinate system has three perpendicular axes and uses ordered triples (x, y, z) to represent a point in space. The typical orientation for the three axes are shown below.

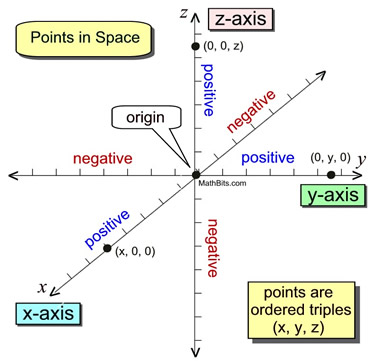This diagram shows both the positive and negative components of the three axes.

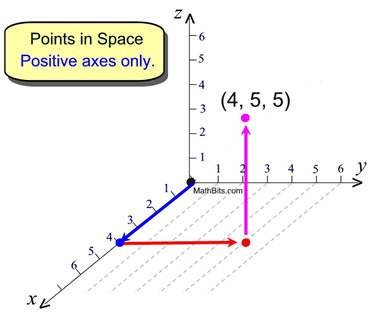You may see 3-D space displayed as only the positive locations on the axes, as shown above. In this space, to plot the point (4,5,5), move 4 units forward along the x-axis, 5 units to the right parallel to the y-axis, and 5 units up, parallel to the z-axis.,

While an equation in two variables represents a line in a plane, an equation in three variables represents a plane in space. So, how hard is it to graph an equation such as x + y - z = 4? Keep in mind that this equation will form a "plane", not a straight line.
ANSWER: It's hard, because it is difficult to visualize 3-D space on a piece of paper.

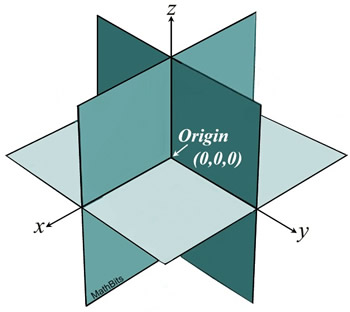
Notice the xy plane, the yz plane and the xz plane in this 3-D coordinate system.. While the 2-D coordinate axis is divided into 4 Quadrants, the 3-D coordinate axis is divided into 8 Octants.

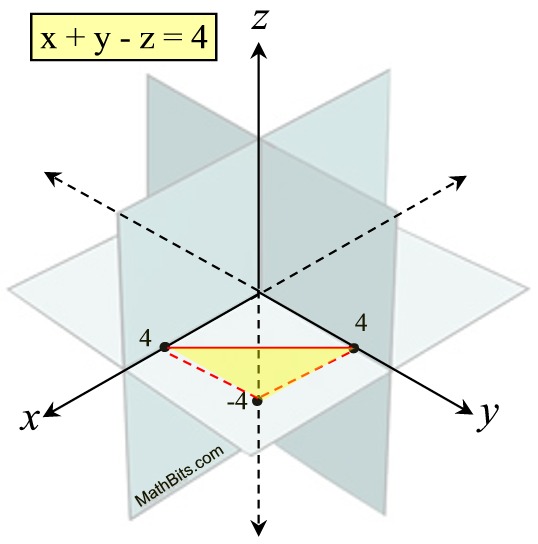To graph this equation, we will establish three points: Let x = 0, y = 0 and find z. Point z is (0,0,-4). Plot. Let y = 0, z = 0 and find x. Point x is (4,0,0). Plot. Let x = 0, z = 0 and find y. Point y is (0,4,0). Plot. Picture the plane that is formed by connecting these 3 points. We want the plane that will cut through the yellow triangle. Remember that a plane goes on indefinitely in all directions.

Note: The following graphical depictions are not exhaustive. There may be other "orientations" of the three planes that illustrate the possible outcomes of "one unique solution", "no solutions", or "infinitely many solutions".

The example above shows the graphing of only one equation. To solve a 3x3 system of equations graphically would require graphing three equations. And the hardest part would be trying to determine where the three planes intersect to determine the final solution to the equations. Graphing is NOT a good method for solving 3x3 systems, unless you have 3-D graphing software that will do the job for you. • Consistent systems have at least one solution. • Inconsistent systems have no solutions. • Independent systems do not share ALL solutions, but can have one point in common. • Dependent systems have ALL solutions of one equation also solutions of the other two equations.

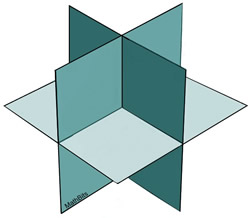
There is ONE unique solution when the planes intersect in one common point. When there is one point common to all three planes, there will be a solution (an ordered triple) to the 3x3 system. Consistent and independent system.

Before we abandon this graphical adventure, let's take a quick graphical look at
some of those "strange" situations that pop up when solving 3x3 systems.

Inconsistent Systems: There are NO solutions. No one point lies in all three planes for any of these situations.
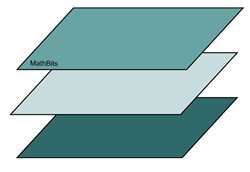
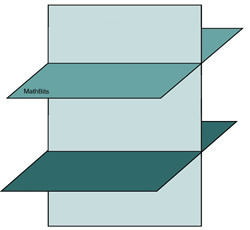
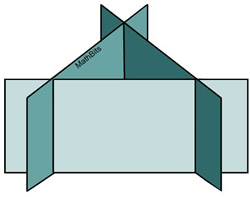
The three planes could be parallel. There will be no intersection point of the 3 planes, and no solution to the 3x3 system.	Two of the planes may be parallel. Again, there is no intersection point of the 3 planes, and no solution to the 3x3 system.	These planes are intersecting, but not in a manner that allows for an intersection point of the three planes. There is no solution to the 3x3 system.
Two planes coinciding and parallel to a third plane also falls into this category. Inconsistent and independent systems.

When using the Elimination Method, if you get rid of all the variables and run into a false numerical statement (such as 0 = 2), you have run into a "strange" graphical situations, such as those shown above, and there will be no solution to the system. "The three planes do not intersect in a single point = no solution."

Dependent System: There are INFINITE solutions. such as when the planes intersect at all points along a common line.
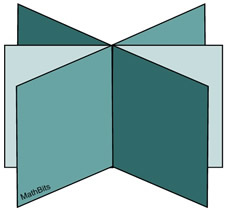
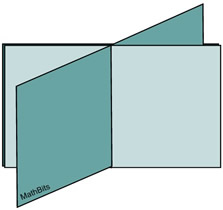
When three distinct planes intersect along a line, there will be an infinite number of solutions to the 3x3 system.	When two of the planes coincide (are the same plane) and intersect with a third plane, there will be an infinite number of solutions to the 3x3 system.	These planes coincide (all three are the same plane). There will be an infinite number of solutions to the 3x3 system. These are consistent, dependent systems.