|
The Multiplication Rule of Probability is used to find
the probability that event A and event B both occur.
The final solution will depend upon whether the two events are independent events, where one event does not affect the other. |
|
In probability, an outcome is in event "A and B"
only when the outcome is in both event A and event B.
(Intersection)
|
|
In a Venn Diagram, an element is in the intersection of "A and B" only when the element is in BOTH sets. |
"AND" is associated with the concept of "BOTH", intersection (overlapping).
You are looking for elements in the sample spaces for events A and B that overlap.
The notation  is used for AND (intersection).
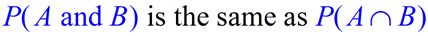
Rules (for AND):
(may be referred to as the "Probability Multiplication Rule"
and is applied when more than one event occurs in succession.)
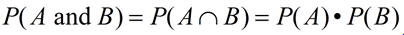
(when A and B are independent events)
P(A and B) = P(A) • P(B | A)
(when A and B are dependent - if A occurs first,
P(A and B) = P(A) • P(B, once A has occurred)
P(A and B) = P(B) • P(A | B)
(when A and B are dependent - if B occurs first,
P(A and B) = P(B) • P(A, once B has occurred)
|
|
 The rule for "AND" must take into account whether the events affect one another.
Actually, there is really only ONE rule, the second rule.
If sets A and B are independent, P(B | A) = P(B) or P(A | B) = P(A).
So, P(A and B) = P(A) • P(B | A) = P(A) • P(B) when A and B are independent.
Or, P(A and B) = P(B) • P(A |B) = P(B) • P(A) when A and B are independent.
 |
. |
A die is rolled and a penny is tossed. What is the probability that a 3 is rolled on the die and a head is tossed on the penny? |
Solution:
Sample space (die) = {1, 2, 3, 4, 5, 6}
Event A: Rolling a 3 on a die: P(A) = 1/6
Sample space (penny)= {H, T}
Event B: Tossing a head with the penny: P(B) = 1/2
Probability of BOTH: These are independent events. Event A does not have an effect on event B.
Answer: P(A and B) = P(A) • P(B) = 1/6 • 1/2 = 1/12 |
 |
 |
. |
Two cards are drawn from a standard deck of cards. What is the probability that the first card is a club and the second card is a heart?
The first card was not put back into the deck after being drawn. |
Solution:
Sample space = {52 cards in the deck}
Event A: Drawing a club: {13 clubs} P(A) = 13/52 = 1/4
Sample space = {51 cards - one card in now missing}
Event B: Drawing a heart: {13 hearts} P(B) = 13/51
Probability of BOTH: These are dependent events. Event B is affected by event A. Without replacing the card, the sample space for the second draw is changed to only 51 available cards.
Answer: P(A and B) = P(A) • P(B | A) = 13/52 • 13/51 = 169/2652
|
Dependent events since the first card was not replaced. |
 |
. |
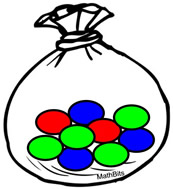
A sack contains 4 green marbles, 3 blue marbles and 2 red marbles. What is the probability of drawing two green marbles in a row if the first marble is returned to the sack before the second draw (with replacement)? |
Solution:
Sample space = {9 marbles}
Event A: Drawing a green marble: P(A) = 4/9
Sample space = {9 marbles}
Event B: Drawing a green marble: P(B) = 4/9
Probability of BOTH: These are independent events. Event B is not affected by event A since the first marble is replaced.
Answer: P(A and B) = P(A) • P(B) = 4/9 • 4/9 = 16/81
|
Independent events since the first marble was replaced. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
