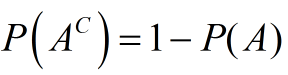|
 |
If A is an event within the sample space S of an experiment, the complement of A (which may be written as AC) consists of all outcomes in S that are not in A.
|
|
The complement of A is everything else in the problem that is NOT in A.
Consider these experiments where an event and its complement are stated:
| Experiment: Tossing a Coin |
| Event |
A |
The coin shows heads. |
| Complement |
AC |
The coin shows tails. |
Experiment: Drawing a Card
The cards in a standard deck are either red or black. |
| Event |
A |
The card is black |
| Complement |
AC |
The card is red |
 |
The probability of the complement of an event is one minus the probability of the event. |
Complement: 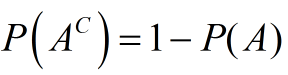 |
|
Since the sum of probabilities of all possible events equals 1, the probability that event A will not occur is equal to 1 minus the probability that event A will occur.


A pair of dice are rolled. What is the probability of not rolling doubles? |
There are 6 ways to roll doubles: (1,1), (2,2), (3,3), (4,4), (5,5) (6,6).
P(doubles) = 6/36 = 1/6
P(not doubles) = 1 - 1/6 = 5/6 |

A pair of dice are rolled. What is the probability of rolling 10 or less? |
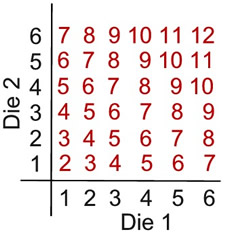 |
The complement of rolling "10 or less" is rolling 11 or 12.
P(10 or less) = 1 - P(11 or 12)
= 1 - [P(11) + P(12)]
= 1 - (2/36 + 1/36) = 33/36 = 11/12 |

 A gum ball machine contains gum balls of five different colors: 36 red, 44 white, 15 blue, 20 green, and 5 orange. The machine dispenser randomly selects one gum ball. What is the probability that the gum ball selected is: A gum ball machine contains gum balls of five different colors: 36 red, 44 white, 15 blue, 20 green, and 5 orange. The machine dispenser randomly selects one gum ball. What is the probability that the gum ball selected is:
a.) green?
b.) not green?
c.) not orange?
d.) orange?
e.) red, white, or blue?
f.) not a color in the flag of the USA?
|
|
There are 120 gum balls in total in the machine.
a.) the probability of green is 20/120 = 1/6.
b.) the probability of not green is 1 - 1/6 = 5/6.
c.) the probability of not orange is 1 - P(orange) = 1 - 5/120 = 1 - 1/24 = 23/24.
d.) the probability of orange is 1/24.
e.) the probability of red, white or blue is 36/120 + 44/120 + 15/120 = 95/120 = 19/24.
f.) find the complement of part e: 1 - 19/24 = 5/24. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|