|
Directions: Grab your paper, pencil and graphing calculator. Find the solution to the following problems. Be sure to show your work where needed.
1. |
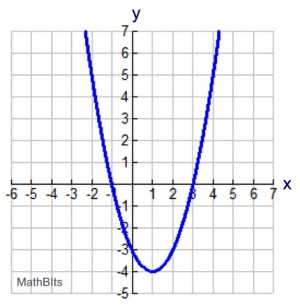
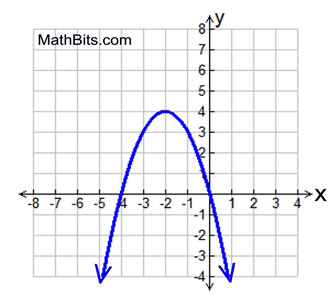
Given f (x) = 3x2+ 6x - 2 and the graph of g(x) shown at the right.
Find the difference between the values of the maximum of
g(x) and the minimum of f (x).
Choose:
|
 |
|
2. |
Which quadratic equation has a minimum value of -12.5 and
x-intercepts of 3 and -2 ?
|
|
|
3. |
Given f (x) = (x - 2)2 - 4, and h(x) as defined by the table below. |
| |
Which of the following statements must be true, based upon this given information?
I: Both f (x) and h(x) have same x-intercepts.
II. Both f (x) and h(x) have y-intercept at y = -4.
|
| x |
h(x) |
| -1 |
0 |
| 0 |
-4 |
| 1 |
-6 |
| 2 |
-6 |
| 3 |
-4 |
| 4 |
0 |
|
|
4. |
The graph of a parabolic function is shown below.
|
"If the equation
(x - 1)2 + (y - 2)2 = 36
is graphed on this same axis,
this new equation will intersect
with the vertex of the parabola."
Is this statement TRUE or FALSE?
|
|
|
|
5. |
Given the equation y = (x - 3)2 + 2.
Which of the features listed below is incorrect regarding this graph? |
|
|
6. |
Regarding the graph of the equation y = x2 - 8x - 20, use the discriminant to determine which statement is true. |
|
|
7. |
Given x2 + y2 = 5 and y = -3x graphed on the same axis.
The point of intersection in Quadrant IV will be ____. |
|
|
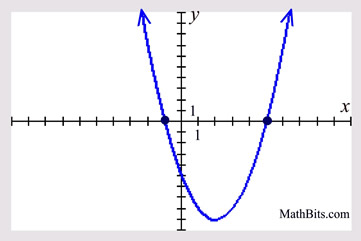
8. Given the graph shown below. Assume integer roots as indicated.
Which statement is TRUE? |
|
 |
|
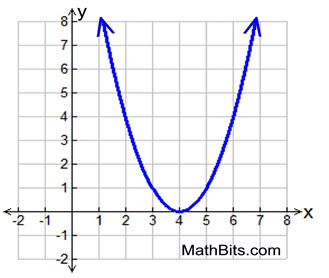
9. |
|
 |
|
10. |
Which fact is not true regarding the graph of y = 4x2 - 6x - 1?
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|