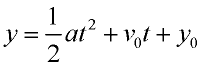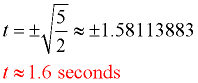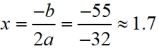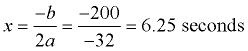|
A projectile is an object that rises and falls under the influence of gravity, and projectile motion is the height of that object as a function of time. Projectile motion can be modeled by a quadratic function. (Air resistance will be ignored in these problems.)
We will be examining the height of projectiles that are "dropped" or "thrown".
Factors that influence the height of an object include the height from which the object is "dropped" or "thrown", whether upward/downward velocity is involved, and of course, the pull of gravity downward on the object.
On Earth, the acceleration due to gravity
is approximately 32 ft/sec2 (or 9.8 m/sec2).
General Formula: |
|
 |
y = height of the projectile
t = time in seconds
a = acceleration due to gravity
v0 = initial (starting) velocity
y0 = initial (starting) height |
FYI: This formula uses ½ the acceleration since acceleration increases over one second, so the average, or ½a, is used.
Notice that this formula is a quadratic function, which means its graph will be a parabola.
 Objects that are dropped: If an object is dropped, it is simply released, and not thrown. There is no initial velocity other than the pull of gravity. This means that the middle term of the formula (seen above) is not needed, since initial velocity (v0) = 0. We will now be using "h" (instead of "y") to represent the height (as it is easier to remember its meaning) and h0 to represent the initial (starting) height.
Working in FEET:
The acceleration due to gravity is -32 ft/sec/sec. (gravity pulls objects toward the Earth making the value negative).
The formula to model the height of an object t seconds after it has been "dropped" is:
 |
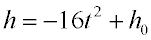Working in METERS:
The acceleration due to gravity is -9.8 meters/sec/sec.
The formula to model the height of an object t seconds after it has been "dropped" is:  |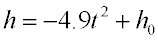
Objects that are thrown: If an object is thrown, a certain amount of initial velocity accompanies its launch. Now, we have a reason to use that middle term from the General Formula (seen above). We will continue to use "h" to represent the height and h0 to represent the initial (starting) height.
Working in FEET:
The acceleration due to gravity is -32 ft/sec/sec.
The formula to model the height of an object t seconds after it has been "thrown" is:
|
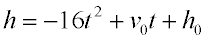
Working in METERS:
The acceleration due to gravity is -9.8 meters/sec/sec.
The formula to model the height of an object t seconds after it has been "thrown" is:
|
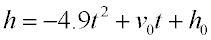
 Object being "dropped":
 |
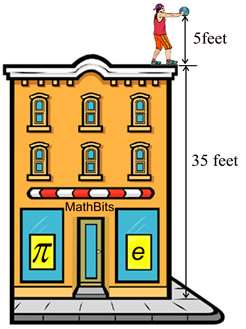Carmine "drops" a ball at shoulder height from the top of a building (as seen at the left). If the ball is at rest, and is simply dropped, how long will it take, to the nearest tenth of a second, to hit the ground?
Solution:
h = -16t2 + h0 The initial height is 40 feet and the height when the ball hits the ground will be 0.
0 = -16t2 + 40
16t2 = 40
t2 = 40/16 = 5/2
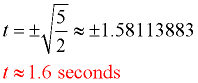
We don't consider "negative" time, so there is only one answer. |
|
|
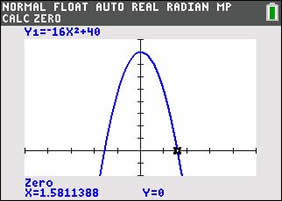
| The graph is NOT the "path" of the ball's horizontal distance traveled.
It is the relationship between the time (x-axis) and the height (y-axis) of the ball at any given time. |
 Object being "thrown":
|
Anton "hits" a baseball at shoulder height (4.5 feet) at an initial velocity of 55 feet per second.
a) How long will it take, to the nearest tenth of a second,for the ball to reach its maximum height?
b) Find the maximum height to the nearest tenth of a foot.
Solution:
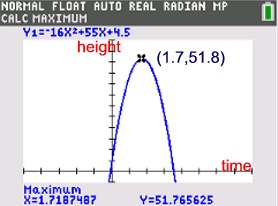
v0 = 55 and h0 = 4.5 and the formula y = -16t2 + 55t + 4.5
y = -16t2 + 55t + 4.5
A parabola reaches its maximum on the axis of symmetry.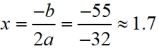
1.7 seconds to reach max.
Substitute in formula for t.
y = 51.8 feet is max height.
|
|
|
| In terms of the "path" of the ball, the graph shows the height of the ball throughout its journey as related to time, but does not show the horizontal "distance" traveled. |
 Object being "thrown" straight up:
A model rocket is "launched" straight upward. The solid fuel propellant pushes the rocket off the ground at an initial velocity of 200 feet per second.
a. When will the rocket reach a height of 336 feet?
b. What is the maximum height reached by the rocket?
c. You forgot to put the parachute in the rocket. When will the rocket hit the ground? |
 |
Solution: Choose the formula h = -16t2 + v0t + h0, which deals with feet and seconds.
The initial velocity, v0 = 200 ft/sec and the initial height is h0 = 0
(since it is launched from the ground).
Formula: h = -16t2 + 200t + 0.
a. Replace h with 336 and solve.
336 = -16t2 + 200t
16t2 - 200t + 336 = 0
8(2t2- 25t + 42) = 0
8 (2t - 21)(t - 2) = 0
2t - 21 = 0; 2t = 21; t = 10.5 sec.
t - 2 = 0; t = 2 sec.
The rocket reaches a height of 336 feet on its way up after 2 seconds and on its way down after 10.5 seconds.
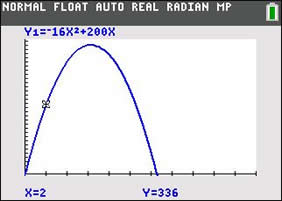
This graph represents the relationship
between time (x-axis) and the height (y-axis)
of the rocket.
|
b. Maximum height?
A parabola reaches its maximum value at its vertex, or turning point. Use the formula for the axis of symmetry to find the
x-coordinate of the vertex.
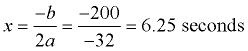
Plug in for t and find h.
h = -16(6.25)2 + 200(6.25) = 625 ft.
The maximum height reached is 625 feet.
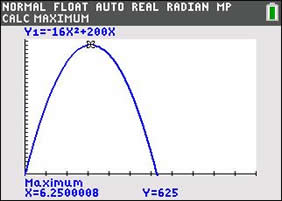
This graph does NOT represent the horizontal path
of the
rocket.
This rocket will theoretically go straight
up
and then fall straight down.
|
c. Hit the ground?
The ground will be a height of 0.
Set the equation equal to 0.
-16t2 + 200t = 0
-8t(2t - 25) = 0
-8t = 0; t = 0 (at launch)
2t - 25 = 0; t = 12.5 sec.
The rocket hit the ground 12.5 seconds after launch. (time/height graph at the right) |
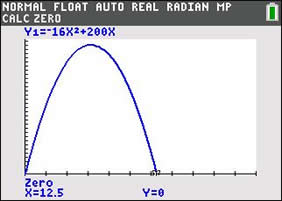
Theoretically, the graph will land at (or near)
the location of its launch.
|
 |
Be careful! As we have seen, these formulas deal with the height
of the projectile over time. It may look like the graph is showing a horizontal path of distance traveled by the projectile, but it is not!
These graphs are showing only the projectiles' heights
at specific moments in time.
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
