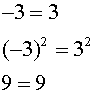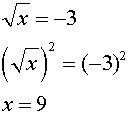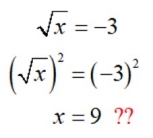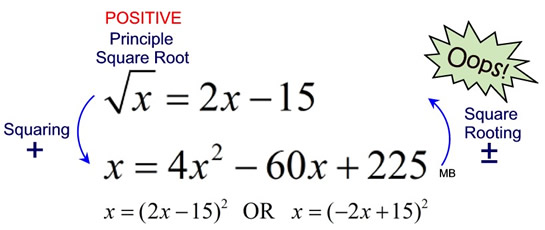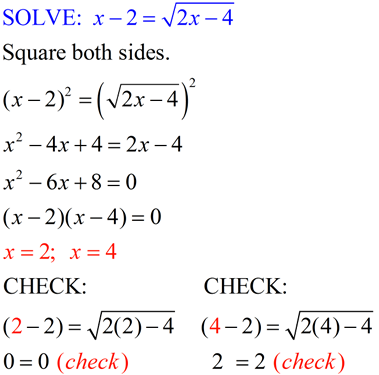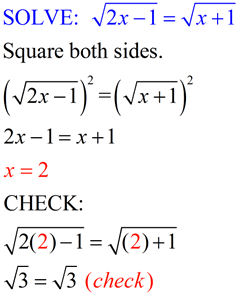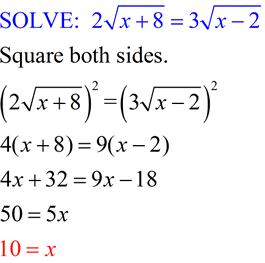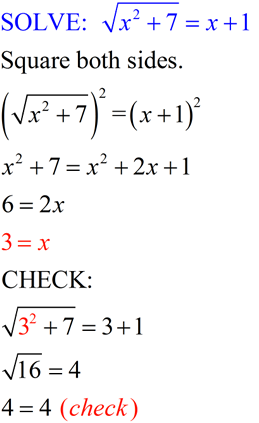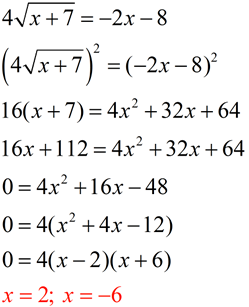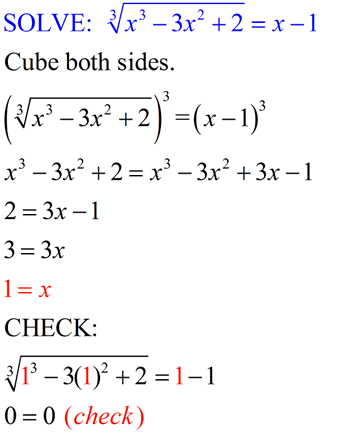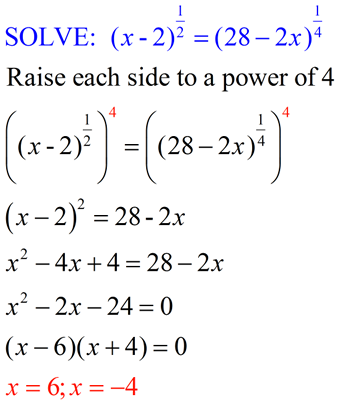|
 |
A radical equation is an equation that has a variable in the radicand
(or a variable with a rational exponent). |
|
On this page, all radicals and expressions with rational exponents represent real numbers.
Assume variables to be positive, real numbers.
The "radical" in a radical equation may be of any root value: square root, cube root, fourth root, etc. This page will concentrate on working with "square root" equations.
 |
Remember that a radical equation has the variable "under" the radical, not simply a numerical radical value within the equation.
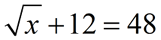 is a radical equation
is a radical equation |
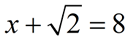 is NOT a radical equation
is NOT a radical equation |
|
|
The solution to a radical equation is a real number which, when substituted for the variable, yields a true equation. Radical equations with square roots can be solved by "squaring", with cube roots by "cubing", and so on. This is an application of inverse operations (where one function will un-do the other). There is an inverse relationship between squaring and square rooting, cubing and cube rooting, etc.
To solve radical equations:
| 1. |
Isolate the radical (or one of the radicals) to one side of the equal sign. |
| 2. |
If the radical is a square root, square each side of the equations. If the radical is not a square root, raise each side to a power equal to the index of the root. (inverse relationships) |
| 3. |
Solve the resulting equation. |
| 4. |
Check your answer(s) to avoid extraneous roots. |
|
|
Square "sides", not "terms".
|
Given 2 + 4 = 6
SQUARE THE SIDES: |
| |
2 + 4 = 6
(2 + 4)² = 6²
36 = 36 |
| DON'T SQUARE THE TERMS, |
| |
2 + 4 = 6
2² + 4² ≠ 6²
4 + 16 ≠36 |
|
This solution process is an application of the principle:
If a and b are real numbers, n is a positive integer, and a = b, then an = bn. |
Finding the solutions, however, get "messier" to find as the indexes increase.

The process of squaring the sides of an equation creates a "derived" equation which may not be equivalent to the original radical equation. Consequently, this new derived equation may create solutions that never previously existed. These "extra" roots that are not true solutions of the original radical equation are called extraneous roots and are rejected as answers.
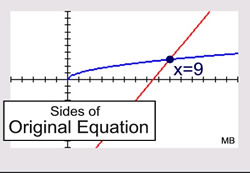
Let's look at this problem of extraneous roots visually. Consider the example from above of 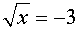
In the first graph below, we see that there is NO solution to this equation since the graphs of the two sides (components) of the equation do not intersect.
In the second graph, we see that graphing the squares of both sides, however, shows that the sides DO intersect, leading to a false conclusion that a real answer (x = 9) exists.
 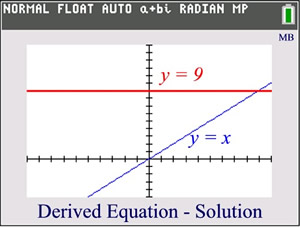
Be on the look-out for these extraneous roots when working with radical functions.
Keep in mind that some of these "perceived" solutions may not actually work
when plugged back into the original equations.
This problem arises from the fact that the converse of the statement:
If a and b are real numbers, n is a positive integer,
and a = b, then an = bn.
is true when n is odd, but not necessarily true when n is even.
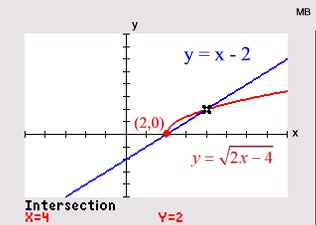
Let's examine another square root situation shown below. We can square both sides of the first radical equation and obtain a true quadratic equation. This new quadratic equation contains not only the square of (2x - 15), but can also contain the square of (-2x + 15), which we do not want. If we take the square root of both sides of the new quadratic equation, we will get two interpretations, 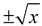 . The new derived equation is yielding more information than we need by offering up extraneous root solutions. . The new derived equation is yielding more information than we need by offering up extraneous root solutions.
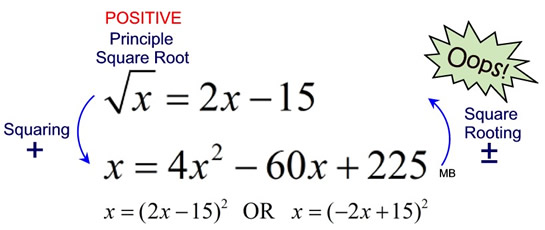
Notice how the graph of the sides of the original radical equation show ONE solution.
The graph of the sides of the new equation shows TWO solutions. The solution of x = 6.25 will not check in the radical equation. |
|
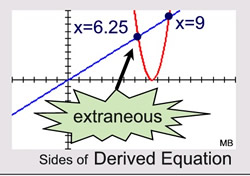 x = 4x2 - 60x + 225
x = 4x2 - 60x + 225 |
CHECKING will be essential to finding correct solutions
(and catching these pesky extraneous roots).
 |
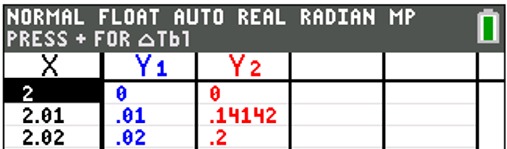
Grab your graphing calculator.
Graph each side of the equation and look for points of intersection. For example, with 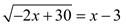 , the algebraic solution will show TWO possible answers. The calculator, however, will verify only ONE actual solution. The second algebraic solution is an extraneous root. , the algebraic solution will show TWO possible answers. The calculator, however, will verify only ONE actual solution. The second algebraic solution is an extraneous root. |
 |
|

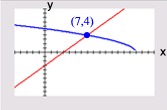
 Example where the answer checks! Example where the answer checks!
 |
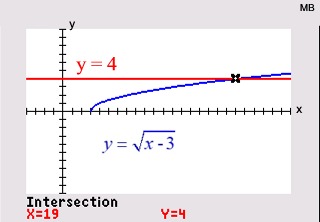 ANSWER: x = 19 ANSWER: x = 19
|
 Example where the answer does NOT check! Example where the answer does NOT check!
 |
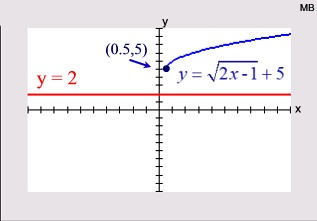
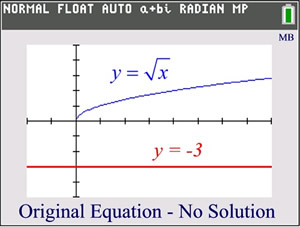
Graphs do not intersect.
No solution. x = 5 is an extraneous root.
ANSWER: no solution
Once the radical was set = -3, it became obvious that there would be NO solution, since the principal square root cannot be a negative value. |
|
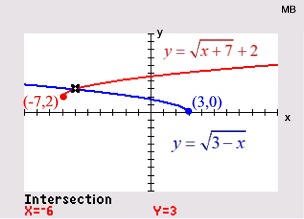
 Example where BOTH answers check! Example where BOTH answers check!
 Example where ONLY ONE answer checks! Example where ONLY ONE answer checks!
 |
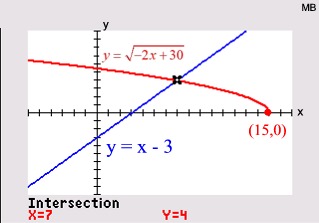
Graph shows only one intersection point.
x = -3 is extraneous root.
ANSWER: x = 7
|
 Example with radicals on BOTH SIDES! Example with radicals on BOTH SIDES!
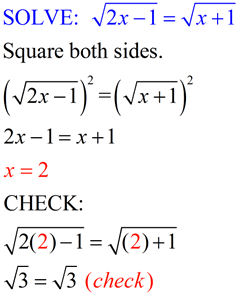 |
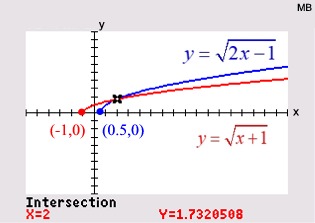
ANSWER: x = 2
|
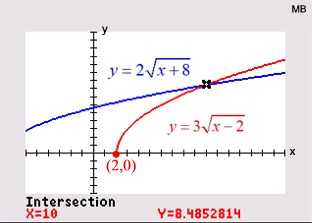
 Example with BOTH radicals multiplied by constants! Example with BOTH radicals multiplied by constants!
 Example involving x2 ! Example involving x2 !
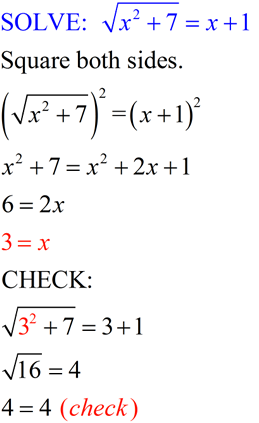 |
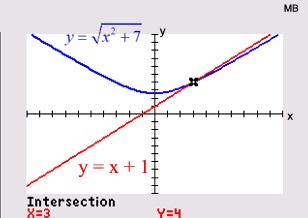 ANSWER: x = 3
ANSWER: x = 3
|
 Example with radicals (and more) on BOTH sides! Example with radicals (and more) on BOTH sides!
 Let's try solving a cube root equation. Let's try solving a cube root equation. |
The concept is the same as we used when working with the square roots, except that now we are cubing instead of squaring.
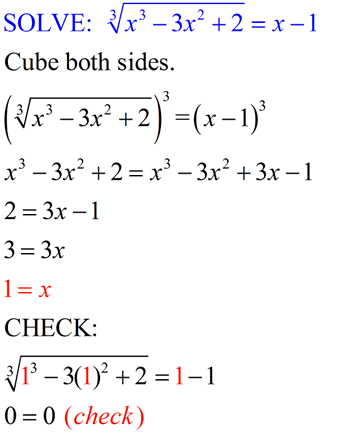 |
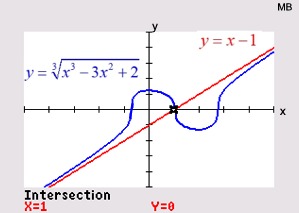 ANSWER: x = 1
ANSWER: x = 1
|

 Let's try solving a rational exponent equation. Let's try solving a rational exponent equation. |
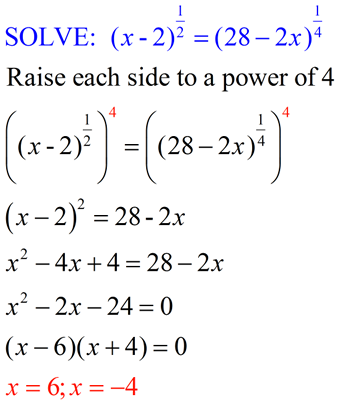

|
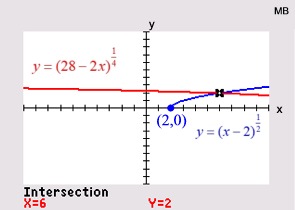 x = -4 is an extraneous root
x = -4 is an extraneous root
ANSWER: x = 6
|

|
For
calculator help with radical
equations.
Click here. |
|
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|