There are a variety of applications of rational expressions and equations, as you will see in the practice sections. On this page, we are going to take a look at two specific types of rational application problems. They are referred to as WORK problems and MOTION problems.

Work Problems:
Problems with two or more people, or machines, working together to complete a task are referred to as work problems.
Work problems are solved by thinking of the situation in the following manner.

|
 |
The part of task completed = rate • time. For example, if Karla can complete the task in 4 hours, she can complete ¼ of the task in 1 hour (which is her "rate").
Example: Karla and Josie both work for a legal data storage company. Working alone, Karla can type a 34 page legal document into the computer in 4 hours. Josie, working alone, can enter the same document into the computer in 6 hours. How long will it take the two women, working together, to enter the document?
Solution: We need to find the time (let x = time in hours) that it will take each woman if they work together to complete the job.
Karla's rate: she can complete 1/4 of the task in one hour.
Josie's rate: she can complete 1/6 of the task in one hour.
Karla's rate • time (x) = 1/4 x
Josie's rate • time (x) = 1/6 x |
Applying the formula shown above, we have:
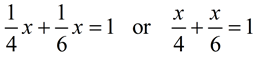
|
Now, we simply solve the rational equation.
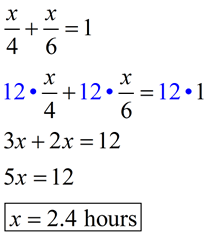 |
Worker |
Rate of Work |
Time Worked |
Part of Task Completed |
Karla |
1/4 |
x |
x/4 |
Josie |
1/6 |
x |
x/6 |
Some people like to prepare a chart of the situation, similar to the one shown above. They then add the last column and set it equal to 1 (representing the whole job completed).
|

Motion Problems:
You are already familiar with the formula:
distance = rate • time
Keep in mind that this formula can also be written:
time = distance / rate |
 |
Example: As an airplane is flying west along with a 20 mph wind, it is able to travel 450 miles in the same amount of time that it could fly east 300 miles against this wind. If it were not for the wind, the plane would be flying at the same speed going east or west. Find the speed of the plane in still air.
Solution: Charts are a popular method for solving these problems.
Let x = the speed of the plane in still air.
Plane |
Distance |
Rate |
Time |
With
wind |
450 |
x + 20 |
450 / (x + 20) |
Against wind |
300 |
x - 20 |
300 / (x - 20) |
|
Since the problem states "in the same amount of time", set the time expressions equal and solve.
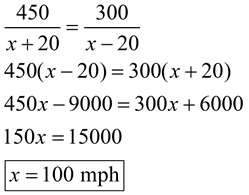
|
|