|
Directions: Read carefully.
1. |
Find this sum using a formula:
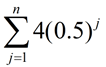
Choose:
|
|
|
2. |
Find the sum of the geometric series:
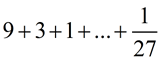
|
|
3. |
In a geometric sequence, the first term is -2 and the common ratio is 3. Find the sum of the first 10 terms.
Choose:
|
|
|
4. |
A culture of bacteria is growing at a rate of 8% per day. There are 160 bacteria in the initial population. With daily observations, how many bacteria, to the nearest bacteria, will have been observed under a microscope in 5 weeks?
Choose:
|
|
|
5. |
The first and fourth terms of a geometric series are 2 and 54 respectively, and all terms are positive. Find the sum of the first 12 terms in this series.
Choose:
|
|
|
6. |
A sequence is defined by the following recursive formula:
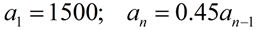 Find the sum of the first 5 terms.
Express answer to nearest tenth. |
|
Choose:
|
|
|
|
7. |
The first three terms of a geometric sequence are (a + 12), a,
and (a - 4) respectively. Find the numerical sum of these first 3 terms.
|
|
Choose:
|
|
|
|
8. |
In a geometric sequence, the common ratio is -5. The sum of the first 3 terms is 147. What is the value of the first term of the sequence?
Choose:
|
|
|
9. |
In a geometric series, the first term is 2 and the common ratio is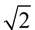 . If the sum of the first n terms of the series is 30(1 + . If the sum of the first n terms of the series is 30(1 +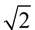 ), what is the value of n? ), what is the value of n?
Choose:
|
|
|
10. |
Starting with the outside triangle, each interior triangle is formed by connecting the 3 midlines (midsegment) of the previous triangle. If the perimeter of the largest triangle is 32, use sigma notation to represent the sum of the perimeters of the largest triangle and the 3 interior triangles formed by the midlines.
|
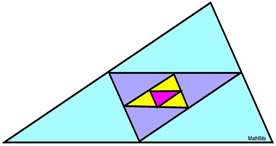 A midline (or midsegment) of a triangle is a segment connecting the midpoints of the sides of a triangle.
A midline (or midsegment) of a triangle is a segment connecting the midpoints of the sides of a triangle. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|