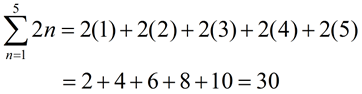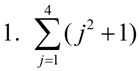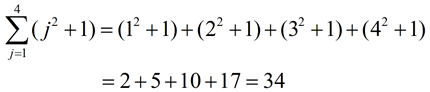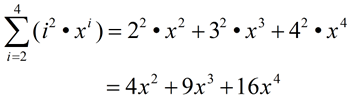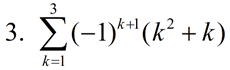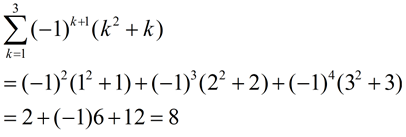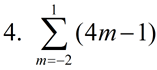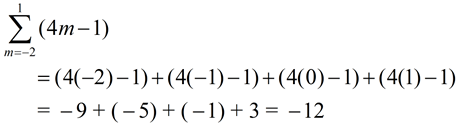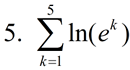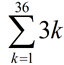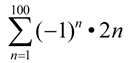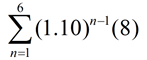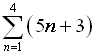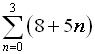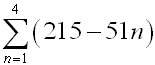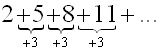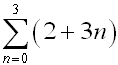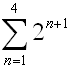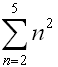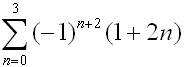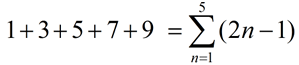|
Consider the finite arithmetic sequence 2, 4, 6, 8, 10.
Now, consider adding these terms together (taking the sum): 2 + 4 + 6 + 8 + 10.
Such a sequence summation is called a series, and is designated by Sn where n represents the number of terms of the sequence being added.
S5 = 2 + 4 + 6 + 8 + 10
This course will be dealing with finite series: sums of a specified number of terms (not infinite sums).
Sn is often called an nth partial sum,
since it can represent the sum of a certain "part" (portion) of a sequence.
A partial sum customarily starts with a1 and ends with an, adding n terms. |
Partial Sums:
S1 = 2
S2 = 2 + 4
S3 = 2 + 4 + 6
S4 = 2 + 4 + 6 + 8
S5 = 2 + 4 + 6 + 8 + 10
|
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
S4 = a1 + a2 + a3 + a4
S5 = a1 + a2 + a3 + a4 + a5
Sn = a1 + a2 + a3 + a4 + a5 + . . . + an
|
The summation of a specified number of terms of a sequence
(a series) can also be represented in a compact form, called summation notation, or sigma notation.
The Greek capital letter sigma ,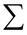 , is used to indicate a sum. , is used to indicate a sum.
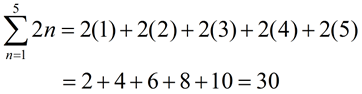
To write the terms of the series, replace n by the consecutive integers
from 1 to 5, as shown above.
|
|

Problem: |
Solution: |
Evaluate:
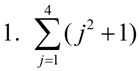 |
Replace j in the expression (j2 + 1) with the values 1, 2, 3 and 4:
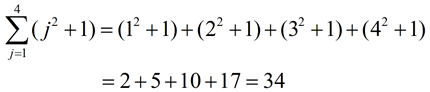
Notice that the expression (j2 + 1) is placed in a set of parentheses behind the sigma. Without the parentheses, only the j2 would be part of the sigma, with the + 1 added on "after" the sigma was completed. |
Evaluate:
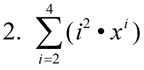
|
Notice that the starting value is i = 2. While the starting value is usually 1, it can actually be any integer value. Also notice how ONLY the variable i is replaced with the values 2, 3, and 4:
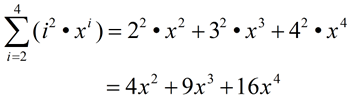 |
Evaluate:
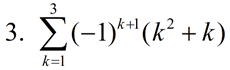 |
This is an important pattern strategy to remember!
Notice how raising (-1) to a power affected by the signs of the terms in the series.
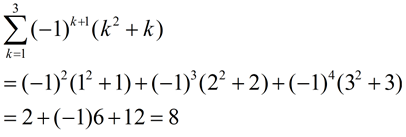 |
Evaluate:
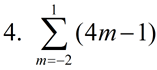
|
Yes, it is possible to calculate a summation on an expression starting with a negative number. Substitute -2, -1, 0 and 1. Remember, however, that when working with sequences, the lowest starting value is 1.
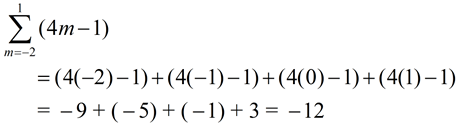
|
Evaluate: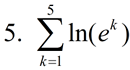
|
OK, so this is a sneaky one. You know that ln( ex) = x, so this summation is the same as 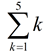 which equals 1 + 2 + 3 + 4 + 5 = 15.
|
6. Use sigma notation to represent
3 + 6 + 9 + 12 + ...
for the first 36 terms. |
Look for a pattern based upon the position of each term. Often making a table will let the pattern to be more easily seen.
Sequence formula:
an = 3n |
position |
term |
1 |
3 |
2 |
6 |
3 |
9 |
4 |
12 |
|
Possible answer:
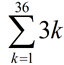 |
|
7. Use sigma notation to represent
-2 + 4 - 6 + 8 - 10 + ...
for the first 100 terms. |
Again, look for a pattern. Remember what we saw in example #3 regarding using powers of (-1) to affect the signs of the terms.
Sequence formula:
an = (-1)n•2n |
position |
term |
1 |
-2 |
2 |
4 |
3 |
-6 |
4 |
8 |
|
Possible answer:
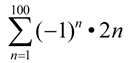 |
|
| 8. Cameron is starting a 6 week jogging program. He will jog 8 miles the first week and increase the distance by 10% per week. Using sigma notation, write an expression to represent the total number of miles he will have jogged over the 6 week program. |
An increase of 10%, is equivalent to 110% per week in the number of miles.
Week 1: 8 miles
Week 2: 8 + .10(8) or 1.10(8) miles
Week 3: 1.10(1.10)(8) = (1.10)2(8)
Week 4: 1.10(1.10)(1.10)
(8) = (1.10)3(8)
(and so on ...) The pattern is
(1.10)n-1(8).
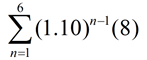 |
 Did you notice that the variable used in the summation symbol (sigma) can be Did you notice that the variable used in the summation symbol (sigma) can be
any letter of your choosing. The sum will be the same, irregardless of the variable used.

Strategies to remember when trying to find an expression for a sequence (series):
Series |
Possible notation
(partial sum) |
Strategy to remember |
|
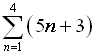 or or 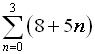 |
Always remember that there is more than one possible answer. |
|
|
Patterns can be either increasing or decreasing. |
|
|
Look to see if a value is being consistently added (or subtracted).
Arithmetic Sequence
|
|
|
Look to see if a value is being consistently multiplied (or divided).
Geometric Sequence |
|
|
Look to see if the values are "famous" numbers such as perfect squares. |
|
|
Look to see if the signs alternate. Alternating signs can be handled using powers of -1. |

Partial Sums Create New Sequences:
The sums (answers) from partial sums of a sequence may form an interesting new sequence. Take a look at the partial sums of the summation of positive odd integers:
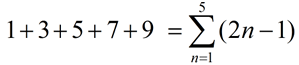
Partial Sums:
S1 = 1 = 1
S2 = 1 + 3 = 4
S3 = 1 + 3 + 5 = 9
S4 = 1 + 3 + 5 + 7 = 16
S5 = 1 + 3 + 5 + 7 + 9 = 25 |
|
The answers from the partial sums create a sequence of perfect squares.
1, 4, 9, 16, 25 |

|
|
For calculator
help with
Summation
Notation (Sigma)
Click here.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|