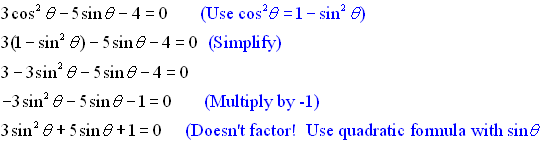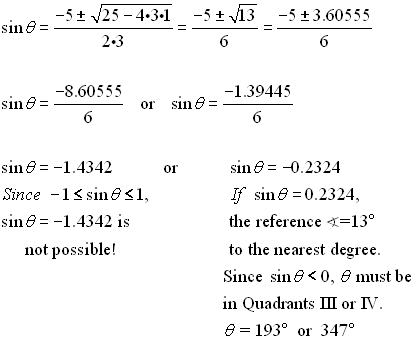When the trig functions has a power (a numerical exponent), it will have to be solved by extracting square roots (cube roots, etc) or by factoring.
Solution:
Solution:
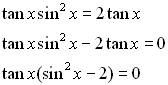 Now, Now, 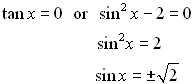
Remember to first solve for the trig function and then solve for the angle value.
Solution:
If there is more than one trig function in the equation, identities are needed to reduce the equation to a single function for solving.
Solution:
There are trig equations, just like there are normal equations, where factoring does not work!! In these cases, the quadratic formula comes in handy.
Solution: Since there are two trig functions in this problem, we need to use an identity Using the quadratic formula, we get:
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|

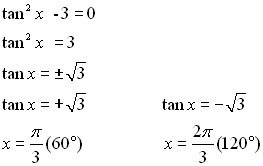
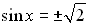 has no solutions.
has no solutions.
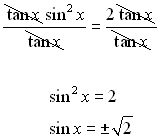
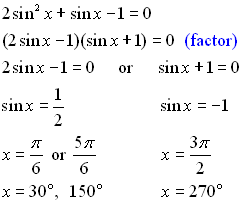
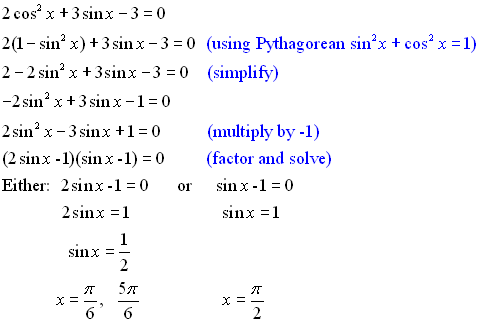
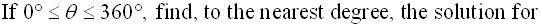
 .
.