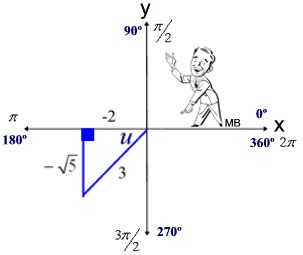
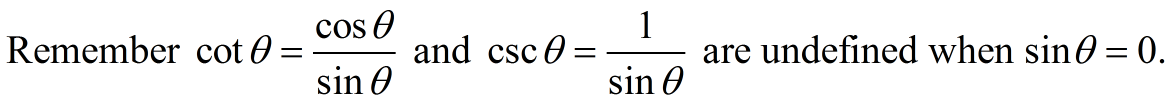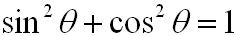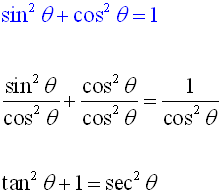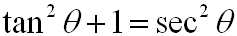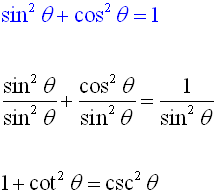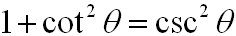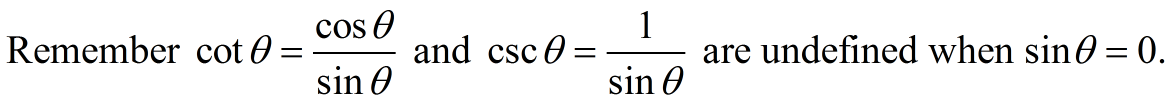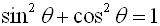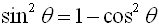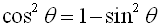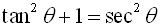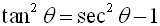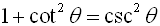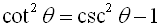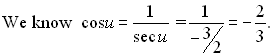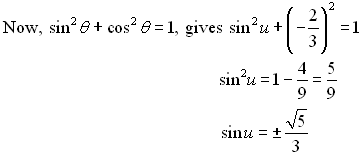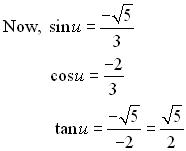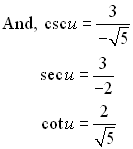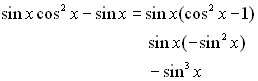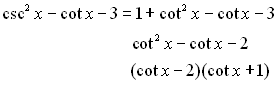This well-known equation is called a
Pythagorean Identity.
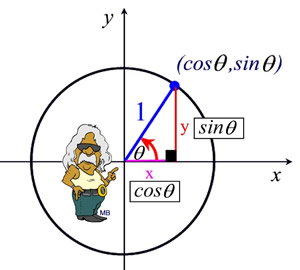
It is true for all values of
θ in the unit circle.
Using this first Pythagorean Identity, two additional Pythagorean Identities can be created.
|
• Start with this first Pythagorean Identity.
• Divide each term by cos2θ.
• We know 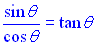 and and 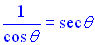 . .
• Substitute and simplify.
|
We now have a second Pythagorean Identity:
It should be noted that there are values of θ for which tangent and secant are undefined.

If we divide by a different value, we can arrive at the third identity:
|
• Start with this first Pythagorean Identity.
• Divide each term by sin2θ.
• We know 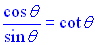 and and 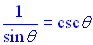 . .
• Substitute and simplify.
|
The third Pythagorean Identity is: