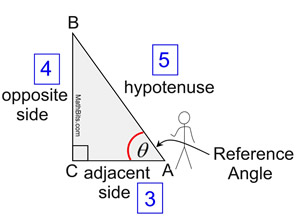
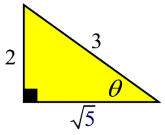
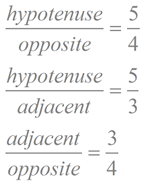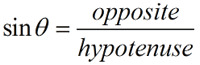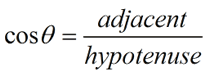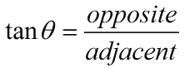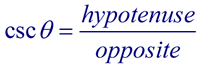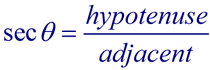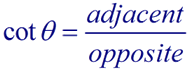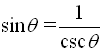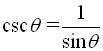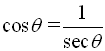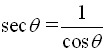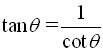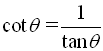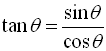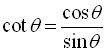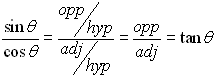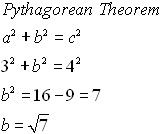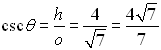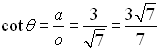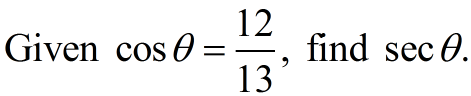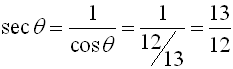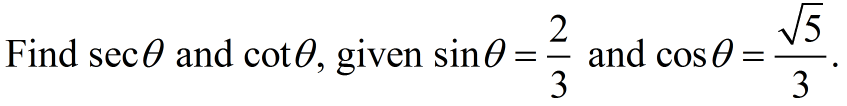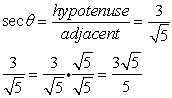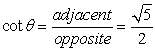In Geometry Trigonometric Functions we saw that there are 3 basic trigonometric ratios. We will now be adding the reciprocals of those ratios to create a total of 6 trigonometric ratios.
So, how many ratios pertaining to the sides of the triangle are possible? Let's take a look:
The first three ratios established above have specific "names" (sine, cosine and tangent). These are referred to as the basic trigonometric functions.
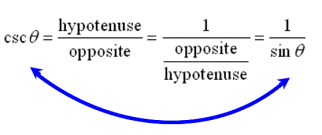
The second three ratios established above also have specific "names" (cosecant, secant, and cotangent). These three ratios are referred to as the reciprocal trigonometric functions.
Notice that these three new ratios are reciprocals of the ratios of the basic trigonometric functions.
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||