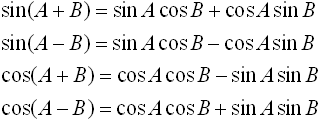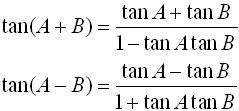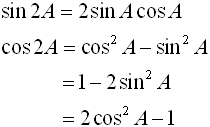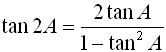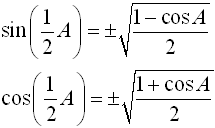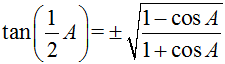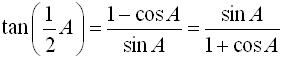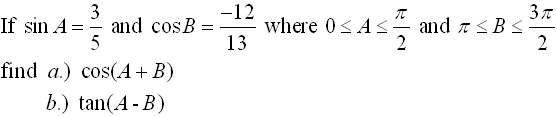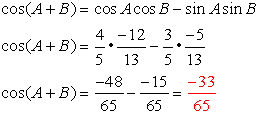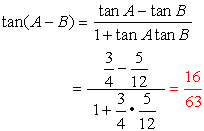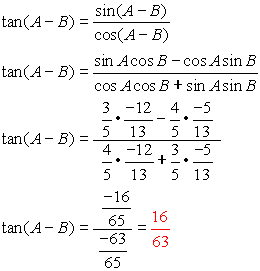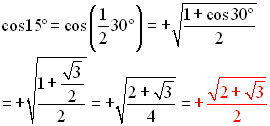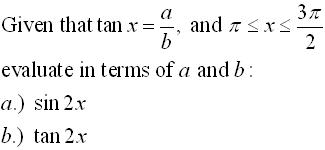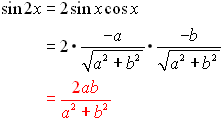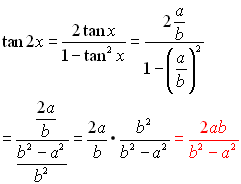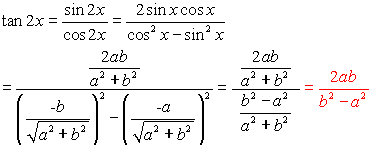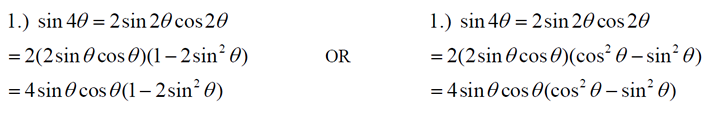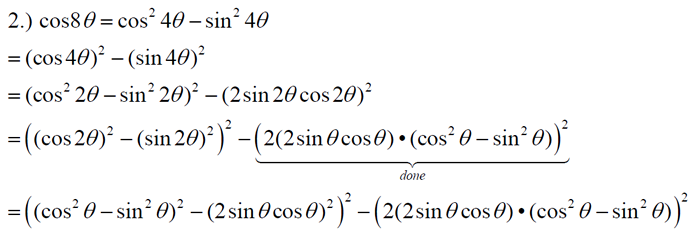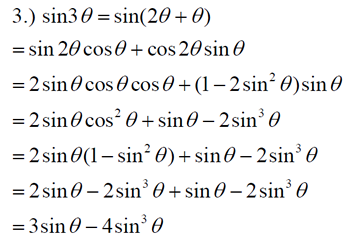Hipparchus, considered to be the most eminent of Greek astronomers (born 160 B.C.),
derived the formulas for the sine and cosine of the sum (or difference) of two angles.
sin(A ± B) and cos(A ± B)
The following formulas (or formulae, in Latin) are trigonometric identities.

Sum and Difference Formulas:

formula30
formula56
Double Angle Formulas:

formula31

formula57
Notice that the double angle formulas can be created by using
the sum formulas for (A + A).
Half Angle Formulas:

formula22

formula1
Or ...

formula55
starbackblue

dividerdash

ex1
formula36
Solution:  The given information produces the triangles shown below.  The Pythagorean Theorem, or a Pythagorean triple, is used to find the missing sides. Using the information from the triangles, find the answers to parts a and b.

a.)
    formula41

b.)
    formula60

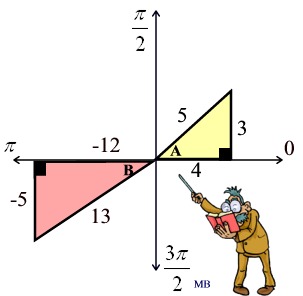
triangle2

What to do if you do not know the tan (A - B) formula!
If you did not know the formula for tan(A - B), the relationship between tangent, sine and cosine can be used to solve this problem.

Simply remember that tan A = sin A / cos A.
Then substitute as shown at the right.

formula42

 

ex2
Using the half angle formula, find the exact value of cos 15º.

Solution:  The positive square root is chosen because cos 15º lies in Quadrant I.
        formula43

 

ex3
formula44
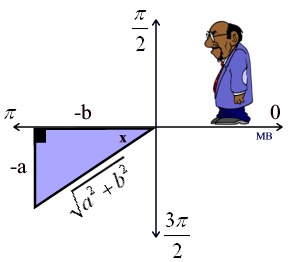
triangle3
Solution:  The given information produces the triangle shown above.  Note the signs associated with a and b.  The Pythagorean Theorem is used to find the hypotenuse.  Using the information from the triangle, find the answers to parts a and b.
a.) formula47 b.) formula59
If you did not know the formula for tan 2x, you could use the relationship between tangent, sine and cosine to find the answer.  This solution at the right will utilize the answer from part a for the numerator. formula46

dividerdash

 

Creating More Identity Formulas

You can use the information you now know about working with trigonometric angles
to create "additional" identity formulas.
For example, the double angle formulas are not restricted to angles
whose values are represented only by θ and 2θ.
Any double combination is valid (such as 2θ and 4θ, or 4θ and 8θ).

(1) sin4θ = 2sin2θ cos2θ
(2) cos8θ = cos24θ - sin24θ

Now, let's play around with these new formulas to see if we can reduce them further.
Simplify these two formulas so that the right hand side of the equation contains only expressions of sinθ and cosθ (not the doubled angles of 2θ or 4θ).

Possible Answers:
       playans1

       playanswer2

dividerdash

Now, let's look at another situation where you are given a new equation and you are asked to verify if this new equation is an identity. Verify that the following new formula equation is an identity.

(3) sin3θ = 3sinθ - 4sin3θ

Possible Answer:
       playanswer3

divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".