|
When working with trigonometric inverse problems, keep the following information in mind:
Inverse Notation: |
arcsin(x) = sin-1(x)
arccos(x) = cos-1(x)
arctan(x) = tan-1(x)
arcsin(x)is read "the angle
whose sine is x".
|
|
|
|

 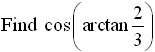 |
 Tangent is positive in Quadrant I.
Tangent is positive in Quadrant I. |
Solution:
You are looking for "the angle whose tangent is" 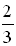 and the angle is in the interval and the angle is in the interval 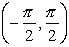 . .
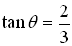 creates the triangle shown at the right. The Pythagorean Theorem was used to find the length of the hypotenuse. creates the triangle shown at the right. The Pythagorean Theorem was used to find the length of the hypotenuse.
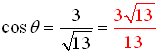 |
 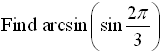 |
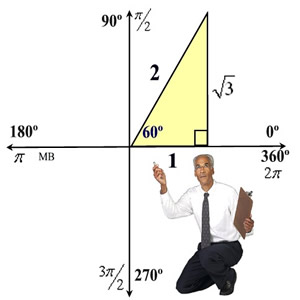
Sine is positive in Quadrant I.
|
Solution:
You are looking for "the angle whose sine is" the same as the 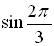 in the interval 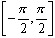 .
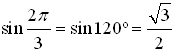
You need to find an angle whose 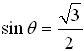
in 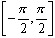 . 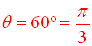 Remember when f (f-1(x)) = x? This concept does not apply in this situation because of the restrictions on the domain of sine inverse.
Remember when f (f-1(x)) = x? This concept does not apply in this situation because of the restrictions on the domain of sine inverse. |

|
For help with trigonometric inverses on
your calculator,
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|