|
Euclidean Geometry is the high school geometry we all know and love!
It is the study of geometry based on definitions, undefined terms (point, line and plane)
and the postulates of the mathematician Euclid (330 B.C.)
Euclid's text, The Elements, was the first systematic discussion of geometry. While many of Euclid's findings had been previously stated by earlier Greek mathematicians, Euclid is credited with developing the first comprehensive deductive system. Euclid's approach to geometry consisted of proving all theorems based upon his five postulates.
Five Postulates of Euclidean Geometry:
1. A straight line segment can be drawn from any given point to any other.
2. Any straight line segment can be extended indefinitely in a straight line.
3. Given any straight line segment, a circle can be dawn having the segment as radius and one endpoint as center.
4. All right angles are congruent.
5. If a straight line crossing two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if extended indefinitely, meet on that side on which are the angles less than the two right angles.
This postulate is equivalent to what is known as the Parallel Postulate. |
Postulates are statements that are accepted as true, but cannot be proven to be true. Over the centuries, mathematicians have endeavored to "prove" Euclid's Fifth Postulate based upon his first four postulates, with no success. In so doing, however, several "equivalent forms" of that Postulate were discovered.
In 1795, John Playfair stated an alternative (equivalent) form of Euclid's Fifth Postulate:
"Through any point in the plane, there is at most one straight line
parallel to a given straight line."
|
This opened the door for naming the Fifth Postulate the Parallel Postulate.

Euclidean Geometry is the study of flat space. We can easily illustrate these geometrical concepts by drawing on a flat piece of paper or chalkboard. In flat space, we know such concepts as:
- the shortest distance between two points is one unique straight line.
|
- the sum of the angles in any triangle equals 180 degrees.
|
|
 |
- the concept of perpendicular to a line can be illustrated as seen in the picture at the right.
|
|
 |
Today, we know the equivalent form of Euclid's fifth postulate,
called the Parallel Postulate, as simply stating:
The Parallel Postulate |
In a plane, at most one line can be drawn through a point not on a given line parallel to the given line. |
|
The concepts in Euclid's geometry remained unchallenged until the early 19th century.
At that time, other forms of geometry started to emerge, called non-Euclidean geometries.
It was no longer assumed that Euclid's geometry could be used to describe all physical space.

non-Euclidean geometry is any form of geometry that contains a postulate (axiom) which is equivalent to the negation of the Euclidean Parallel Postulate.
1. Riemannian Geometry (also called elliptic geometry or spherical geometry) is a non-Euclidean geometry using as its Parallel Postulate any statement equivalent to the following:
"If l is any line and P is any point not on l ,
then there are no lines through P that are parallel to l ." |
Riemannian Geometry is named for the German mathematician, Bernhard Riemann, who in 1889 rediscovered the work of Girolamo Saccheri (Italian) showing certain flaws in Euclidean Geometry. |
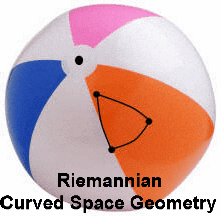
Riemannian Geometry is the study of curved surfaces. Consider what would happen
if instead of working on the Euclidean flat piece of paper, you work on a curved surface,
such as a sphere (or a beach ball).
The study of Riemannian Geometry has a direct connection to our daily existence
since we live on a curved surface called planet Earth.
 |
What effect does working on a sphere, or a curved space, have on what we think of as geometrical truths?
- In curved space, the sum of the angles of any triangle is now always greater than 180°.
- On a sphere, there are no straight lines. As soon as you start to draw a straight line, it curves on the sphere.
|
| • |
In curved space, the shortest distance between any two points (called a geodesic) is not unique. For example, there are many geodesics between the north and south poles of the Earth (lines of longitude) that are not parallel since they intersect at the poles.
|
•
|
In curved space, the concept of perpendicular to a line can be illustrated as seen in the picture at the right. |
 |

2. Hyperbolic Geometry (also called saddle geometry or Lobachevskian geometry) is a non-Euclidean geometry using as its Parallel Postulate any statement equivalent to the following:
"If l is any line and P is any point not on l ,
then there exists at least two lines through P that are parallel to l ". |
Lobachevskian Geometry is named for the Russian mathematician, Nicholas Lobachevsky, who, like Riemann, furthered the studies of non-Euclidean Geometry. |
| Hyperbolic Geometry is the study of a saddle shaped space. Consider what would happen if instead of working on the Euclidean flat piece of paper, you work on a curved surface shaped like the outer surface of a saddle or a Pringle's potato chip. |
 |
 |
What effect does working on a saddle shaped surface have on what we think of as geometrical truths?
- In hyperbolic geometry, the sum of the angles of a triangle is less than 180°.
- In hyperbolic geometry, triangles with the same angles have the same areas.
|
| • |
There are no similar triangles in hyperbolic geometry.
|
•
|
In hyperbolic space, the concept of perpendicular to a line can be illustrated as seen in the picture at the right. |
 |
| • |
Lines can be drawn in hyperbolic space that are parallel (do not intersect).
Actually, many lines can be drawn parallel to a given line through a given point.
|
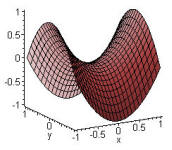
Graphically speaking, the hyperbolic saddle shape is
called a hyperbolic paraboloid, as seen at the right. |
 |
It has been said that some of the works of artist M. C. Escher illustrate hyperbolic geometry.
In his work Circle Limit III , the effect of a hyperbolic space's negative curve on the sum of the angles in a triangle can be seen. Escher's print illustrates a model devised by French mathematician Henri Poincare for visualizing the theorems of hyperbolic geometry,
the orthogonal circle.

 |
Now, aren't you glad we are
working in Euclidean Geometry! |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|









