Geometric Properties of Equality MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

In Algebra, we saw a Real Numbers Property Chart.
The first entries in that chart were the properties most used in algebraic problem solving:
distributive property, commutative property, associative property, identity property,
inverse property, and closure property.
(refer to the Real Number Property Chart if you need to review these properties)

It is understood that all of the properties in the Real Numbers Property Chart are
of importance in Algebra, Geometry, and future mathematics courses.

In Geometry, we will be focusing more on the "equality properties of numbers"
from that chart, with those properties stated in geometric terms.

	Property	Geometric Examples	Verbal hints
14.	Addition Property of Equality	If AB = CD, and EF, then AB + EF = CD + EF If AB = CD, and EF = GH then AB + EF = CD + GH	"adding the same value to both sides of an equation will not change the truth value of the equation." "when equals are added to equals, the sums are equal"
15.	Subtraction Property of Equality	If AB = CD, and EF, then AB - EF = CD - EF If AB = CD, and EF = GH then AB - EF = CD - GH	"subtracting the same value from both sides of an equation will not change the truth value of the equation." "when equals are subtracted from equals the results are equal."
16.	Multiplication Property of Equality	If AB = CD, then 2 • AB = 2 • CD	"multiplying both sides of an equation by the same value will not change the truth value of the equation."
17.	Division Property of Equality (non-zero denominator)	If AB = CD, then AB / 2 = CD / 2	"dividing both sides of an equation by the same non-zero value will not change truth value of the equation."
18.	Substitution Property	If AB + CD = 42, and CD = 20 then AB + 20 = 42	"a value may be substituted for its equal."
19.	Reflexive (or Identity) Property of Equality	AB = AB	"a real number is always equal to itself"
20.	Symmetric Property of Equality	If AB = CD, then CD = AB	"quantities that are equal can be read forward or backward"
21.	Transitive Property of Equality	If AB = CD and CD = EF, then AB = EF.	"if two numbers are equal to the same number, then the two numbers are equal to each other"
22.	Law of Trichotomy	If AB > 8, then AB 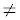8 and AB is not < 8.	"for two real numbers a and b, a is either equal to b, greater than b, or less than b." (common sense)

Most of these properties appear as "common sense" in relation to
what we already know about working with number values.

In Geometry, these properties will also come into play as reasons in "proofs",
to verify statements we need to make to support the solution.