|
For more in-depth information about each of these angles see Circles.

1. Central Angle
A central angle is an angle formed by two radii
with the vertex at the center of the circle.
Central Angle = Intercepted Arc
 |
In the diagram at the right, ∠AOB is a central angle with an intercepted minor arc from A to B.
|
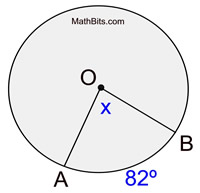
m∠AOB = 82º |
|
2. Inscribed Angle
An inscribed angle is an angle with its vertex
"on" the circle, formed by two intersecting chords.
Inscribed Angle = 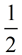 Intercepted Arc Intercepted Arc
 |
In the diagram at the right, ∠ABC is an inscribed angle with an intercepted minor arc from A to C.
|
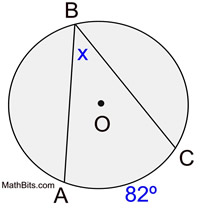 m∠ABC = 41º
m∠ABC = 41º |
|
3. Tangent Chord Angle
An angle formed by an intersecting tangent and chord
has its vertex "on" the circle.
Tangent Chord Angle = 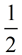 Intercepted Arc Intercepted Arc
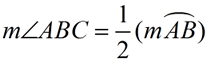 |
In the diagram at the right, ∠ABC is an angle formed by a tangent and chord with an intercepted minor arc from A to B.
|
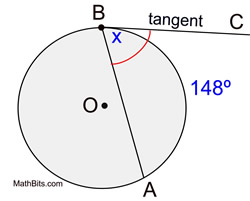 m∠ABC = 74º m∠ABC = 74º |
|
4. Angle Formed by Two Intersecting Chords |
When two chords intersect inside a circle, four angles are formed. At the point of intersection, two sets of congruent vertical angles are formed in the corners of the X that appears.
Angle Formed by Two Chords
= 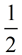 (SUM of Intercepted Arcs) (SUM of Intercepted Arcs)
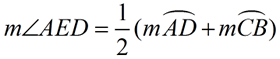 |
|
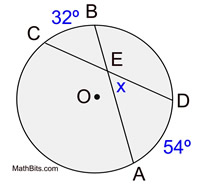 m∠AED = 43º
m∠AED = 43º
|
Also, m∠BEC = 43º (vertical angle)
m∠CEA and m∠BED = 137º by straight angle formed.
|
|
5. Angle Formed Outside of Circle by Intersection:
"Two Tangents" or "Two Secants" or a "Tangent and a Secant".
The formulas for all THREE of these situations are the same:
Angle Formed Outside = 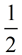 ( DIFFERENCE of Intercepted Arcs)
|
|
∠ ABC is formed by two tangents intersecting outside of circle O.
The intercepted arcs are major arc 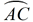
and minor arc 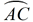 .
These two arcs together comprise the entire circle.
Angle Formed by Two Tangents
= 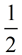 (DIFFERENCE of Intercepted Arcs) (DIFFERENCE of Intercepted Arcs)
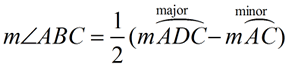
(When subtracting, start with the larger arc.)
|
|
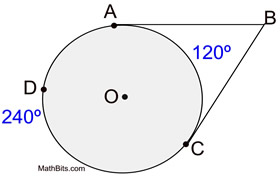
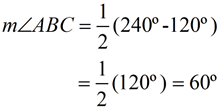 m∠ABC = 60º
m∠ABC = 60º |
|
| |
∠ CAE is formed by two secants intersecting outside of circle O.
The intercepted arcs are major arc 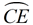 and minor arc 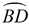 .
Angle Formed by Two Secants
= 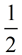 (DIFFERENCE of Intercepted Arcs) (DIFFERENCE of Intercepted Arcs)
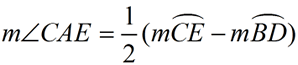
(When subtracting, start with the larger arc.)
|
|
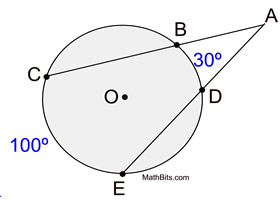
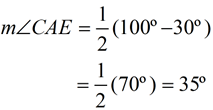
m∠CAE = 35º
|
|
| |
∠ BAD is formed by a tangent and a secant intersecting outside of circle O.
The intercepted arcs are arc 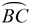 and arc 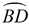 .
Angle Formed by Tangent and Secant
= 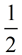 (DIFFERENCE of Intercepted Arcs) (DIFFERENCE of Intercepted Arcs)
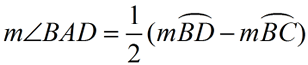
(When subtracting, start with the larger arc.)
|
|
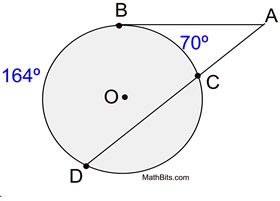
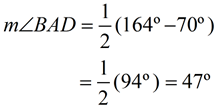
m∠BAD = 47º
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
